Çevrel Çemberin Merkezi
Çevrel Çember (Çevrel Çember Nedir?) Bir üçgenin üç köşe noktasından da geçen veya üç köşe noktasını da üzerinde bulunduran çembere "çevrel çember" veya "üçgeni

Pow
@powÇevrel Çember (Çevrel Çember Nedir?)
Bir üçgenin üç köşe noktasından da geçen veya üç köşe noktasını da üzerinde bulunduran çembere "çevrel çember" veya "üçgenin çevrel çemberi" denir.
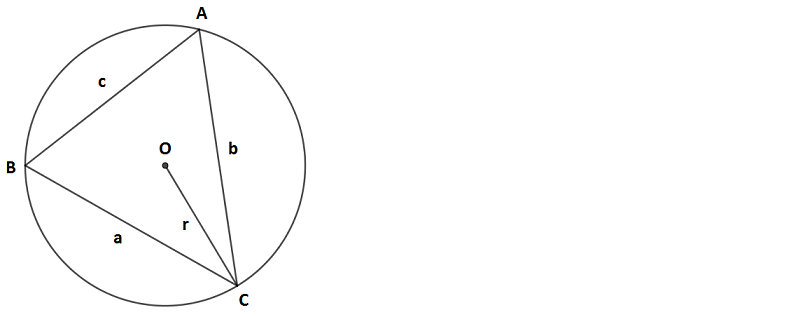
Yukarıdaki şekildeki O merkezli r yarıçaplı çember, ABC üçgeninin köşe noktalarından geçen veya köşe noktalarını üzerinde bulunduran ABC üçgeninin bir çevrel çemberidir.
Çevrel Çemberin Merkezini Neresidir?
Bir üçgenin çevrel çemberinin merkezi herhangi iki kenar orta dikmesinin kesiştiği noktadır. Bir üçgenin herhangi bir kenarıyla doksan derecelik bir açı yapan ve bu kenarı tam orta noktasında kesen doğruya orta dikme denir.
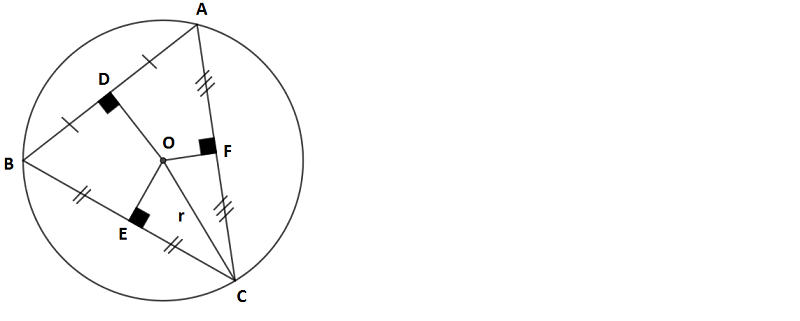
Yukarıdaki şekildeki ABC üçgeninin O merkezli r yarıçaplı çevrel çemberinin merkezi, kenarlarını kesen orta dikmelerinin kesiştiği noktadır.
İspat
Bir ikizkenar üçgende üçüncü kenara ait yükseklik, açıortay, kenarortay ve orta dikme kesişir.
Yukarıdaki şekildeki ABC üçgeni ikiz kenar bir üçgendir. Üçgenin A köşesinden BC kenarına inilen dikme ([AD] doğru parçası) hem açıortay, hem kenarortay, hem yükseklik hem de orta dikmedir.
Yukarıdaki şekildeki ABC üçgeni, ikiz kenar bir üçgen olup |AB| = |AC| ve m (B) = m (C)'dir. Buna göre; ABD ve ACD üçgenleri Açı - Açı - Açı bakımından benzer üçgenlerdir. Yukarıdaki şekilden de kolayca anlaşılacağı üzere (İki açısı birbirine eşit olan iki üçgenin üçüncü açıları da birbirine eşit olur) BC kenarına indiğimiz dikme A açısını iki eşit parçaya böler. Yine yukarıdaki şekilden kolayca anlaşılacağı üzere ABD ve ACD üçgenleri A. A. A. bakımından benzer ve ikişer kenarları aynı uzunlukta olduğundan üçüncü kenarları da üçgenlerde benzerlik kurallarına göre aynı uzunlukta olmak zorunda olacağı için [AD] doğru parçası BC kenarına iki eşit parçaya böler. Üçgenin herhangi bir köşesinden karşısındaki kenara inilen dikme o kenara ait yükseklik olacağı için [AD] doğru parçası üçgenin BC kenarına ait yüksekliğidir. Üçgenin herhangi bir köşesinden karşısındaki kenara inilen dikme eğer o kenarı iki eşit parçaya bölüyorsa bu dikmeye orta dikme denir. Yukarıdaki şekildeki [AD] doğru parçası BC kenarının orta dikmesidir.
Yukarıdaki şekilde üç tane ikiz kenar üçgen bulunmakta olup (OAB, OBC ve OCA üçgenleri birer ikiz kenar üçgendir) bunların eşit olmayan kenarlarına indireceğimiz orta dikmelerin ortak başlangıç noktası ancak ve ancak şekilden de anlaşılacağı üzere çevrel çemberin merkezi olabilir.
Çevrel Çemberinin Yarıçapı Bilinen Bir Üçgenin Alanını Bulma
a, b, c üçgenin kenar uzunlukları ve r çevrel çemberin yarıçapı olmak üzere yukarıdaki ABC üçgenin alanı;
A (ABC) = a . b . c / 4 . r'dir.
İspat
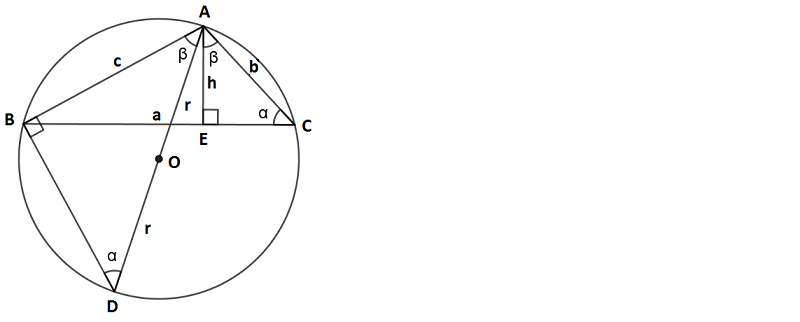
Yukarıdaki şekilde O merkezli r yarıçaplı çember, ABC üçgeninin çevrel çemberidir. Bir çemberde aynı yayı gören çevre açıların ölçüleri birbirine eşit olacağı için C açısının ölçüsü ile D açısının ölçüsü birbirine eşittir (m (C) = m (D) = α). İki açısı birbirine eşit olan ABD ve AEC üçgenlerinin üçüncü açıları da birbirine eşit olacağı için BAD açısının ölçüsü ile EAC açısının ölçüsü birbirine eşit olur (m (BAD) = m (DEAC = β). Buna göre ABD ile AEC üçgenleri Açı - Açı - Açı bakımından benzer üçgenlerdir. Üçgenlerde benzerlik kurallardan faydalanarak aşağıdaki bağıntıları yazabiliriz.
AB / AD = AE / AC
c / 2r = h / b
2r . h = b . c
h = b . c / 2r olur.
A (ABC) = a . h / 2
A (ABC) = a . b . c / 2r / 2
A (ABC) = a . b . c / 4r olur.
Published Date:
December 05, 2020
Updated Date:
December 11, 2023