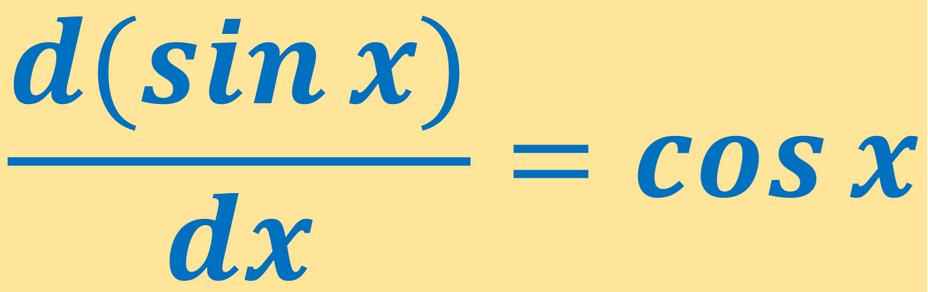Какова Производная от Sin x?
Производная от sin x равна cos x.
(sin x)′=cos x
dxd(sin x)=cos x
Доказательство Производной от Sin x
Метод 1
f′ (x)=h→0limhf (x+h)−f (x)
(sin x)′=h→0limhsin (x+h)−sin x
sin (p+q)=sin p.cos q+cos p.sin q
(sin x)′=h→0limhsin x.cos h+cos x.sin h−sin x
(sin x)′=h→0limhsin x.cos h−sin x+cos x.sin h
(sin x)′=h→0limhsin x.(cos h−1)+cos x.sin h
(sin x)′=h→0lim [hsin x.(cos h−1)+hcos x.sin h]
(sin x)′=h→0limhsin x.(cos h−1)+h→0limhcos x.sin h
(sin x)′=sin x.h→0limhcos h−1+cos x.h→0limhsin h
t→0limtsin t=1 t→0limtcos t−1=0
(sin x)′=sin x.0+cos x.1
(sin x)′=0+cos x
(sin x)′=cos x
Метод 2
f′ (x)=h→0limhf (x+h)−f (x)
(sin x)′=h→0limhsin (x+h)−sin x
sin p−sin q=2.sin 2p−q.cos 2p+q
(sin x)′=h→0limh2.sin 2x+h−x.cos 2x+h+x
(sin x)′=h→0limh2.sin 2h.cos 22x+h
(sin x)′=h→0limh2.sin 2h.cos 22.(x+2h)
(sin x)′=h→0limh2.sin 2h.cos (x+2h)
(sin x)′=h→0lim21.hsin 2h.cos (x+2h)
(sin x)′=h→0lim2hsin 2h.cos (x+2h)
(sin x)′=h→0lim [2hsin 2h.cos (x+2h)]
(sin x)′=h→0lim2hsin 2h.h→0limcos (x+2h)
h→0 (2h=h)
(sin x)′=h→0limhsin h.h→0limcos (x+h)
(sin x)′=1.cos (x+0)
(sin x)′=1.cos x
(sin x)′=cos x
Метод 3
sin x=x−3!x3+5!x5−7!x7+9!x9−...
cos x=1−2!x2+4!x4−6!x6+8!x8−...
sin x=x−3!x3+5!x5−7!x7+9!x9−...
(sin x)′=(x−3!x3+5!x5−7!x7+9!x9−...)′
(sin x)′=(x)′−(3!x3)′+(5!x5)′−(7!x7)′+(9!x9)′−...
(sin x)′=1−3!3x2+5!5x4−7!7x6+9!9x8−...
(sin x)′=1−3.2!3x2+5.4!5x4−7.6!7x6+9.8!9x8−...
(sin x)′=1−2!x2+4!x4−6!x6+8!x8−...
(sin x)′=cos x
Метод 4
eix=cos x+i.sin x
(cos x+i.sin x)′=(eix)′
(cos x)′+(i.sin x)′=(eix)′
(cos x)′+i.(sin x)′=(eix)′
(eu)′=u′.eu
(cos x)′+i.(sin x)′=(ix)′.eix
(cos x)′+i.(sin x)′=i.eix
(cos x)′+i.(sin x)′=i.(cos x+i.sin x)
(cos x)′+i.(sin x)′=i.cos x+i2.sin x
i2=−1
(cos x)′+i.(sin x)′=i.cos x+(−1).sin x
(cos x)′+i.(sin x)′=i.cos x+(−sin x)
(cos x)′+i.(sin x)′=−sin x+i.cos x
(sin x)′= cos x
Published Date:
January 05, 2025
Updated Date:
April 24, 2025