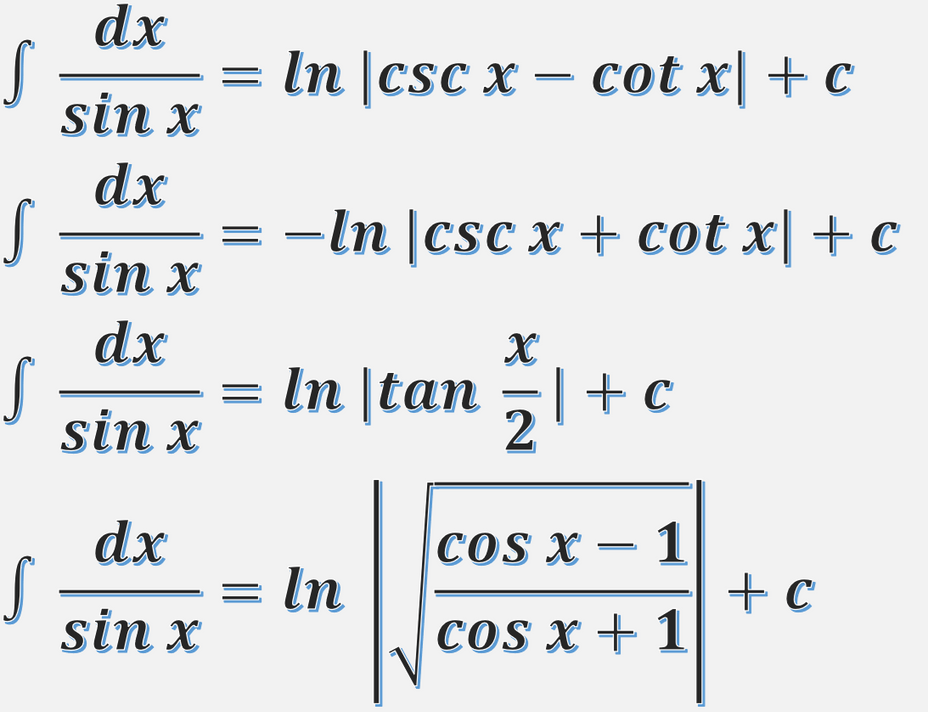1/Sin x'in İntegrali Nedir ?
∫sin xdx=−ln ∣csc x+cot x∣+c=ln ∣csc x−cot x∣+c=ln ∣tan 2x∣+c=ln ∣cos x+1cos x−1∣+c
1/Sin x'in İntegralini Bulma
1. Yol
sin x1=csc x
∫sin xdx=∫csc x dx
∫sin xdx=∫csc x+cot xcsc x.(csc x+cot x) dx
∫sin xdx=∫csc x+cot xcsc2 x+csc x.cot x dx
csc x+cot x=u
d (csc x+cot x)=du
(csc x+cot x)′ dx=du
(csc x)′ dx+(cot x)′ dx=du
(csc x)′=−csc x.cot x (cot x)′=−(1+cot2 x)=−sin2 x1=−csc2 x
−csc x.cot x dx−csc2 x dx=du
(−csc x.cot x−csc2 x) dx=du
−(csc x.cot x+csc2 x) dx=du
(csc x.cot x+csc2 x) dx=−du
∫sin xdx=∫u−du
∫sin xdx=−∫udu
∫xdx=ln ∣x∣+c
∫sin xdx=−ln ∣u∣+c
∫sin xdx=−ln ∣csc x+cot x∣+c
∫sin xdx=ln ∣(csc x+cot x)−1∣+c
∫sin xdx=ln ∣csc x+cot x1∣+c
∫sin xdx=ln ∣(csc x−cot x)(csc x+cot x)csc x−cot x∣+c
∫sin xdx=ln ∣csc2 x−cot2 xcsc x−cot x∣+c
csc x=sin x1 cot x=sin xcos x
∫sin xdx=ln ∣(sin x1)2−(sin xcos x)2csc x−cot x∣+c
∫sin xdx=ln ∣sin2 x1−sin2 xcos2 xcsc x−cot x∣+c
∫sin xdx=ln ∣sin2 x1−cos2 xcsc x−cot x∣+c
1−cos2 x=sin2 x
∫sin xdx=ln ∣sin2 xsin2 xcsc x−cot x∣+c
∫sin xdx=ln ∣csc x−cot x∣+c
2. Yol
∫sin xdx=∫sin xsin x.sin x1 dx
∫sin xdx=∫sin x.sin xsin x.1 dx
∫sin xdx=∫sin2 xsin x dx
sin2 x=1−cos2 x
∫sin xdx=∫1−cos2 xsin x dx
cos x=u
d (cos x)=du
(cos x)′ dx=du
(cos x)′=−sin x
−sin x dx=du
sin x dx=−du
∫sin xdx=∫1−u2−du
∫sin xdx=∫u2−1du
∫sin xdx=∫(u−1).(u+1)du
(u−1).(u+1)1=u−1A+u+1B
(u−1).(u+1)1=(u−1).(u+1)A.(u+1)+B.(u−1)
(u−1).(u+1)1=(u−1).(u+1)Au+A+Bu−B
0.u+1=(A+B).u+A−B
A+B=0
A−B=1
A+B+A−B=0+1
2A=1
A=21
21+B=0
B=0−21=−21
∫sin xdx=∫u−11/2 du+∫u+1−1/2 du
∫sin xdx=∫u−11/2 du−∫u+11/2 du
∫sin xdx=21∫u−1du−21∫u+1du
∫sin xdx=21(∫u−1du−∫u+1du)
∫x±adx=ln ∣x±a∣
∫sin xdx=21(ln ∣u−1∣−ln ∣u+1∣)+c
∫sin xdx=21ln ∣u+1u−1∣+c
∫sin xdx=ln ∣(u+1u−1)21∣+c
∫sin xdx=ln ∣u+1u−1∣+c
∫sin xdx=ln ∣cos x+1cos x−1∣+c
3. Yol
sin2 x+cos2 x=1
sin 2x=2.sin x.cos x
∫sin x1 dx=∫2.sin 2x.cos 2xsin2 2x+cos2 2x dx
∫sin xdx=∫(2.sin 2x.cos 2xsin2 2x+2.sin 2x.cos 2xcos2 2x) dx
∫sin xdx=∫2.sin 2x.cos 2xsin2 2x dx+∫2.sin 2x.cos 2xcos2 2x dx
∫sin xdx=∫2.sin 2x.cos 2xsin 2x.sin 2x dx+∫2.sin 2x.cos 2xcos 2x.cos 2x dx
∫sin xdx=∫21.cos 2xsin 2x dx+∫21.sin 2xcos 2x dx
∫sin xdx=21∫cos 2xsin 2x dx+21∫sin 2xcos 2x dx
cos xsin x=tan x sin xcos x=cot x
∫sin xdx=21∫tan 2x dx+21∫cot 2x dx
∫tan ax dx=a1ln ∣cos ax1∣+c
∫cot ax dx=a1ln ∣sin ax∣+c
∫sin xdx=21.211ln ∣cos 21x1∣+21.211ln ∣sin 21x∣+c
∫sin xdx=21.12ln ∣cos 2x1∣+21.12ln ∣sin 2x∣+c
∫sin xdx=ln ∣cos 2x1.sin 2x∣+c
∫sin xdx=ln ∣cos 2xsin 2x∣+c
∫sin xdx=ln ∣tan 2x∣+c
Published Date:
May 09, 2021
Updated Date:
April 17, 2025