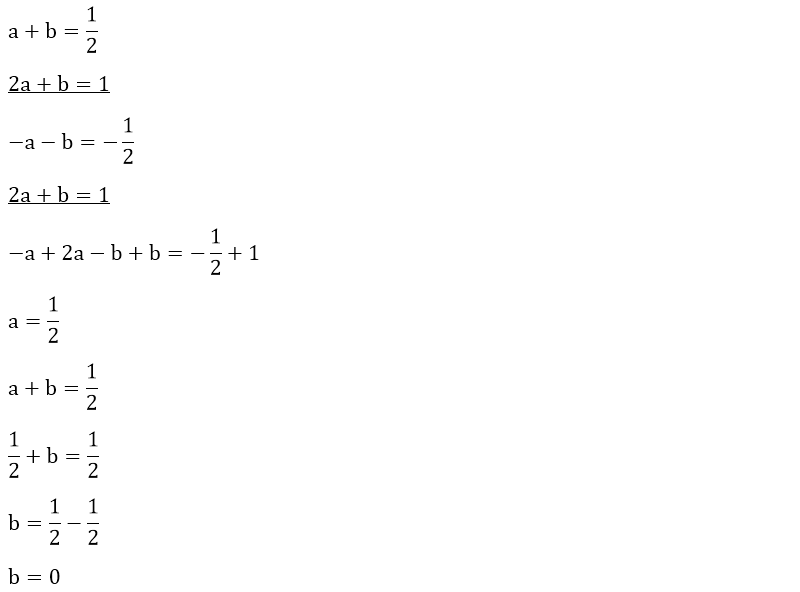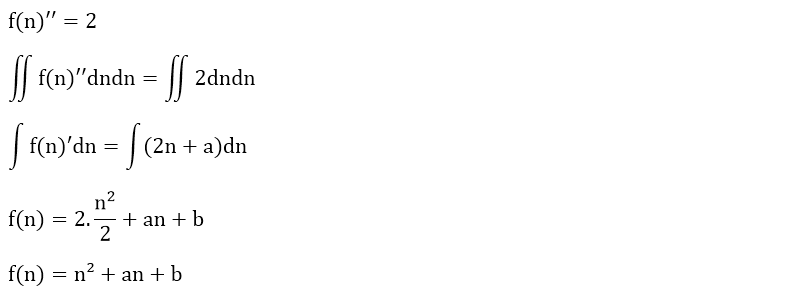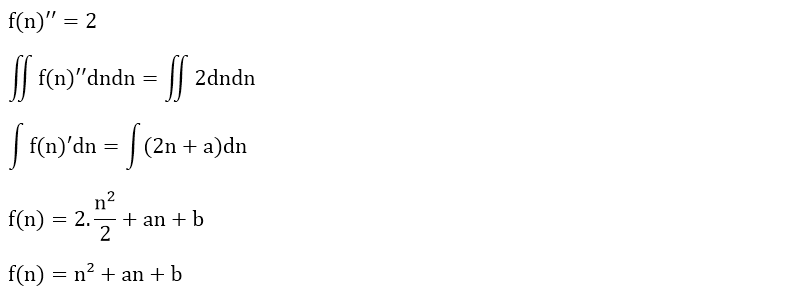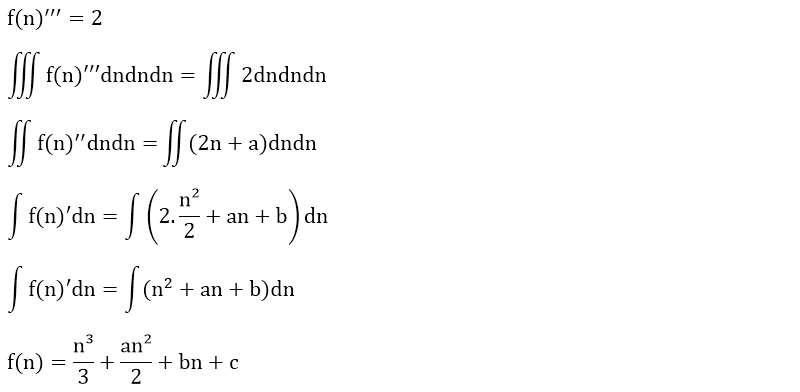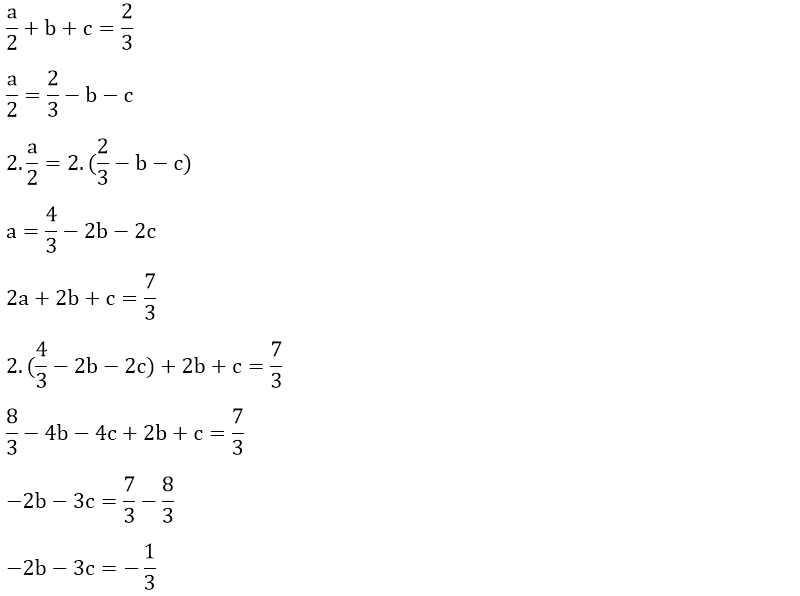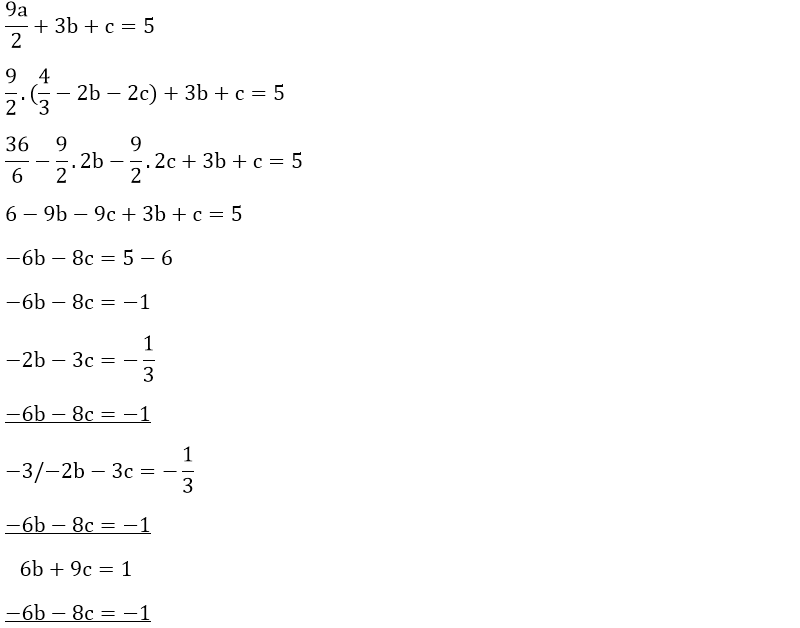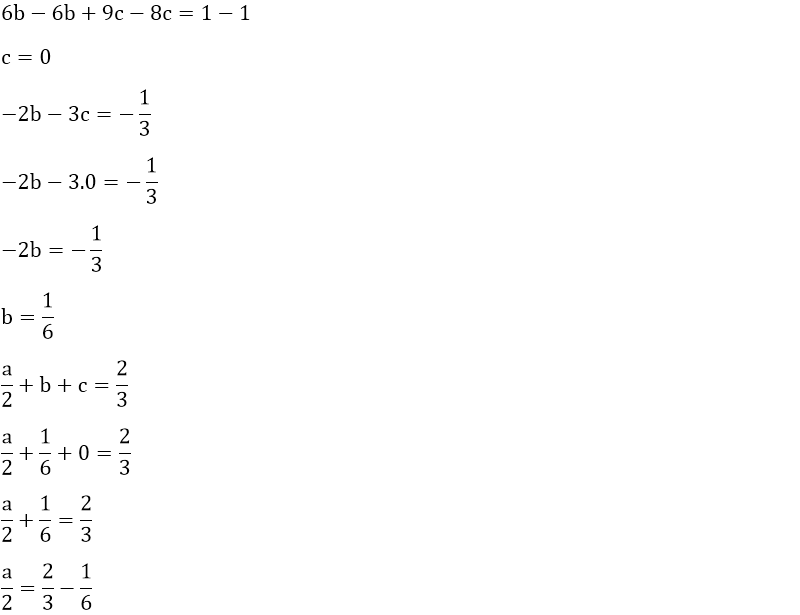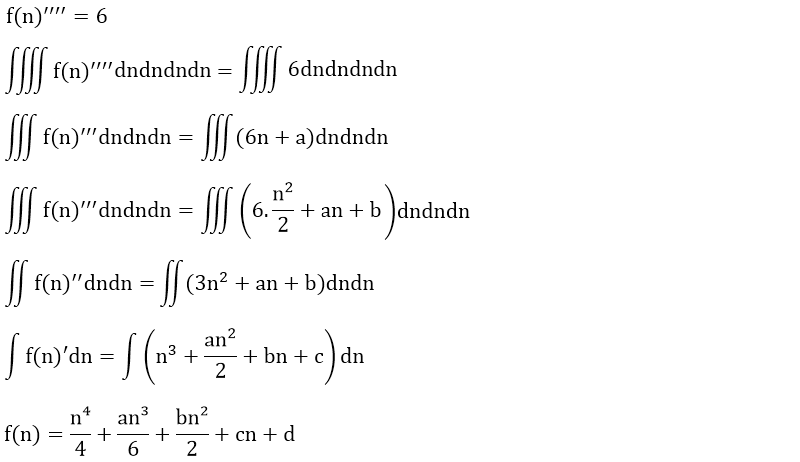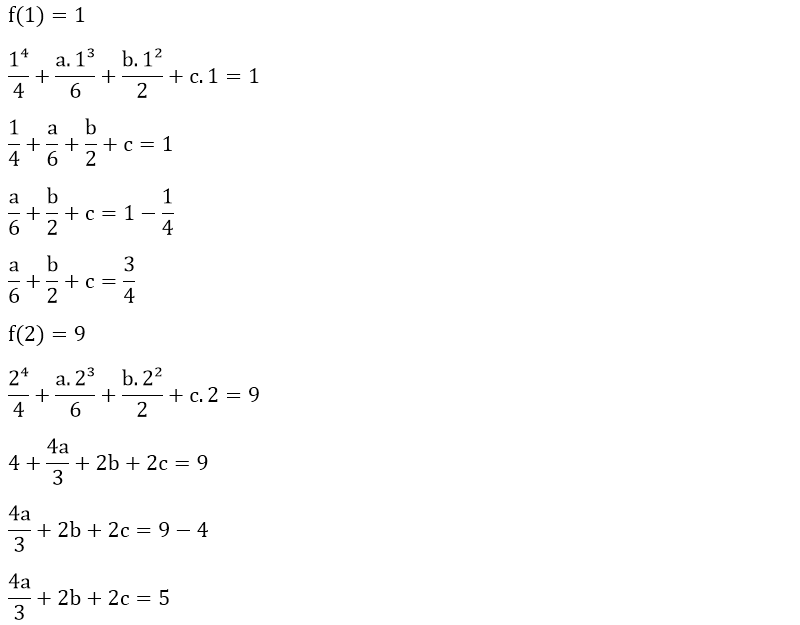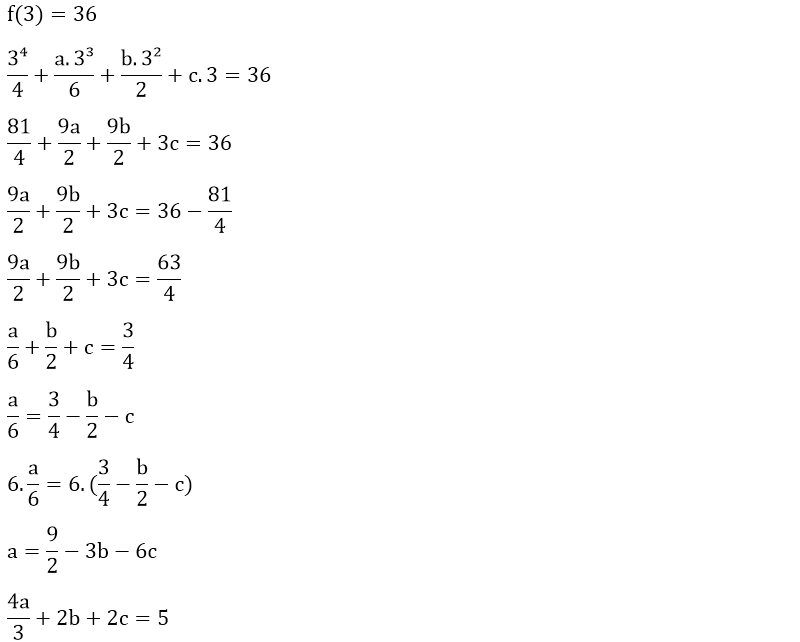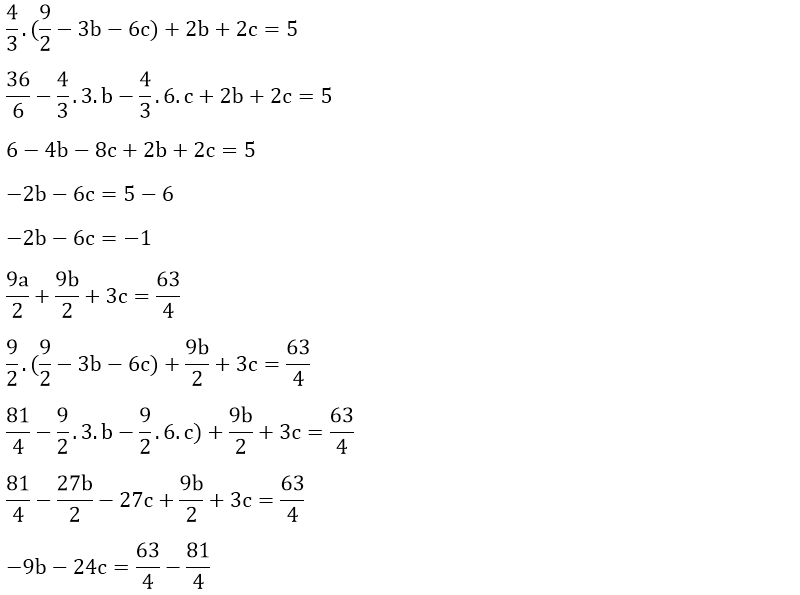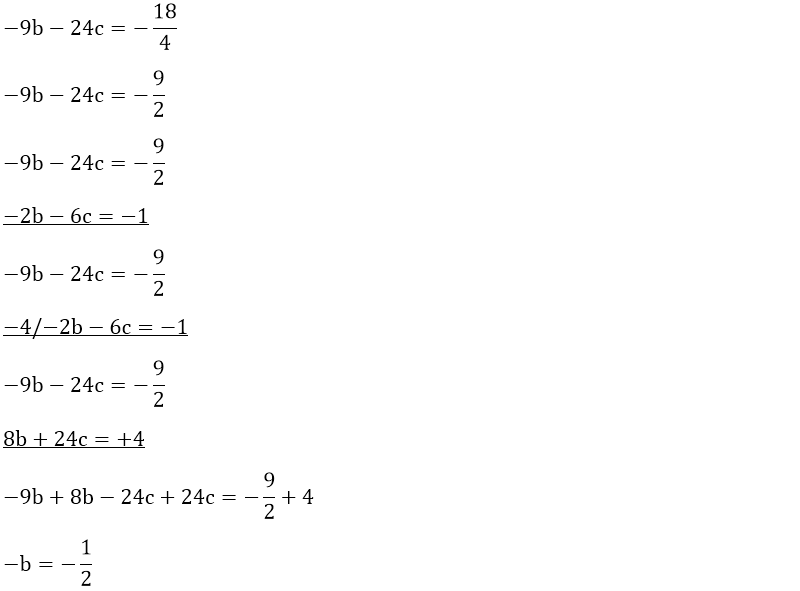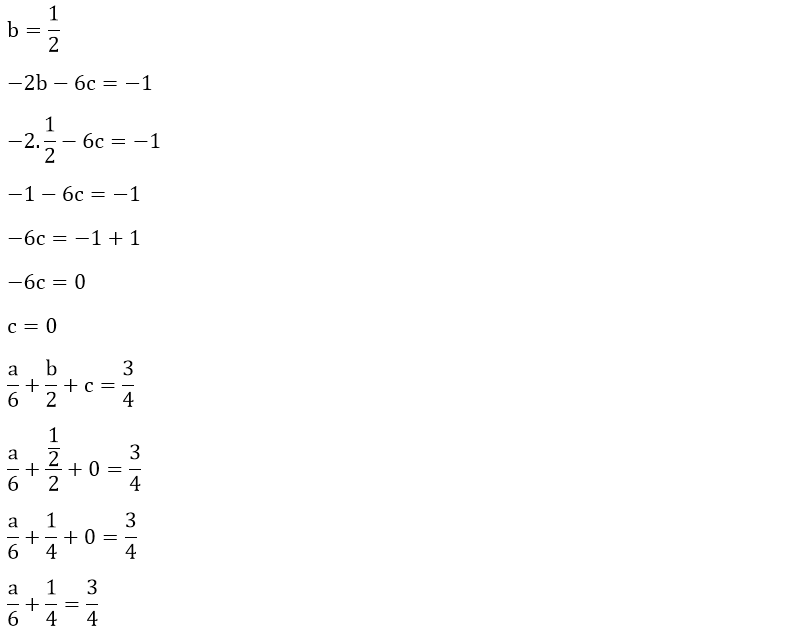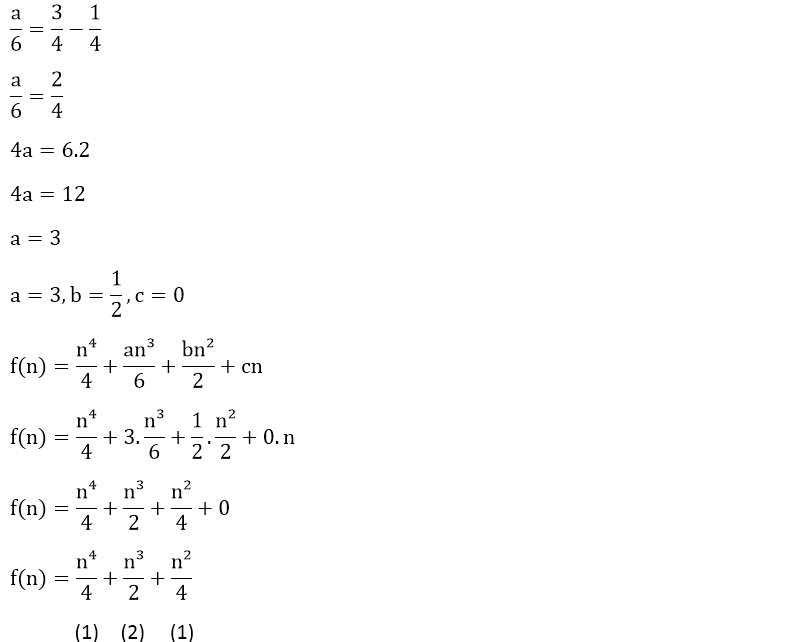Ardışık Sayıların Toplamı | Toplam Formülü

Kendisinden önce ve sonra gelen sayılara belli bir kural ile bağlı olan sayılara ardışık sayı denir.

Örneğin, aşağıdaki dizileri oluşturan sayılar birer ardışık sayıdır.

1, 2, 3, ... , n (Art arda gelen iki terim arasında hep 1 fark var)

1, 3, 5, ... , 2n - 1 (Art arda gelen iki terim arasında hep 2 fark var)

2, 4, 6, ... , 2n (Art arda gelen iki terim arasında hep 2 fark var)

Ardışık Sayılarda Terim Sayısı

Terim Sayısı = (Son Terim - İlk Terim)/Artış Miktarı + 1

Ardışık Sayıların Toplamı

(Son Terim + İlk Terim) . (Terim Sayısı)/2

Toplam Formülü

Ardışık sayılardan ve ardışık olmayan ama belirli bir kurala göre oluşturulan sayılardan meydana gelen dizilerin genel toplam formüllerini çok katlı integral ve türev yardımı ile de bulabiliriz.

Bir fonksiyon da fonksiyonun iki değişkeni arasındaki birinci fark fonksiyonun birinci türevini, ikinci fark ikinci türevini, üçüncü fark üçüncü türevini ve dördüncü fark ise dördüncü türevini verecek şekilde devam eder gider.

1. 1 + 2 + 3 + ... + n = n . (n + 1) / 2

İspat

f(n) = 1 + 2 + 3 + ... + n olsun.

f(1) = 1

2

f(2) = 3 1

3 0

f(3) = 6 1 0

4 0

f(4) = 10 1

5

f(5) = 15

Yukarıdaki f(n) fonksiyonunun ikinci türevi f(n)'' sabit bir sayı olan 1’e eşittir. İlk önce eşitliğin her iki tarafının da çift katlı (iki katlı) belirsiz integralini alalım.

f(n) fonksiyonumuzun genel denklemini bulduktan sonra sıra a ve b değerlerini bulmaya geldi.

2. 2 + 4 + 6 + ... + 2n = n . (n + 1)

İspat

f(n) = 2 + 4 + 6 + ... + 2n olsun.

f(1) = 2

4

f(2) = 6 2

6 0

f(3) = 12 2 0

8 0

f(4) = 20 2

10

f(5) = 30

Yukarıdaki f(n) fonksiyonunun ikinci türevi f(n)'' sabit bir sayı olan 2’ye eşittir. İlk önce eşitliğin her iki tarafının da çift katlı (iki katlı) belirsiz integralini alalım.

f(n) fonksiyonumuzun genel denklemini bulduktan sonra sıra a ve b değerlerini bulmaya geldi.

3. 1 + 3 + 5 + ⋯+ 2n - 1 = n²

İspat

f(n) = 1 + 3 + 5 + ... + 2n - 1 olsun.

f(1) = 1

3

f(2) = 4 2

5 0

f(3) = 9 2 0

7 0

f(4) = 16 2

9

f(5) = 25

Yukarıdaki f(n) fonksiyonunun ikinci türevi f(n)'' sabit bir sayı olan 2’ye eşittir. İlk önce eşitliğin her iki tarafının da çift katlı (iki katlı) belirsiz integralini alalım.

f(n) fonksiyonumuzun genel denklemini bulduktan sonra sıra a ve b değerlerini bulmaya geldi.

4. 1² + 2² + 3² + ... + n² = n . (n + 1) . (2n + 1) / 6

İspat

f(n) = 1² + 2² + 3² + ... + n² olsun.

f(1) = 1

4

f(2) = 5 5

9 2

f(3) = 14 7 0

16 2 0

f(4) = 30 9 0

25 2

f(5) = 55 11

36

f(6) = 91

Yukarıdaki f(n) fonksiyonunun üçüncü türevi f(n)''' sabit bir sayı olan 2’ye eşittir. İlk önce eşitliğin her iki tarafının da üç katlı belirsiz integralini alalım.

f(n) fonksiyonumuzun genel denklemini bulduktan sonra sıra a, b ve c değerlerini bulmaya geldi.

Yukarıdaki birinci dereceden üç bilinmeyenli denklem sisteminde yok etme metodunu kullanarak a, b ve c değerlerini kolaylıkla bulabiliriz.

Örneğin, a değerini yok ederek denklemimizi çözmeye çalışalım.

5.1³ + 2³ + 3³ + ⋯ + n³ = [n . (n + 1 ) / 2]²

İspat

f(n) = 1³ + 2³ + 3³ + ⋯ + n³ olsun.

f(1) = 1

8

f(2) = 9 19

27 18

f(3) = 36 37 6

64 24 0

f(4) = 100 61 6 0

125 30 0

f(5) = 225 91 6

216 36

f(6) = 441 127

343

f(7) = 784

Yukarıdaki f(n) fonksiyonunun dördüncü türevi f(n)'''' sabit bir sayı olan 6’ya eşittir. İlk önce eşitliğin her iki tarafının da dört katlı belirsiz integralini alalım.

f(n) fonksiyonumuzun genel denklemini bulduktan sonra sıra a, b, c ve d değerlerini bulmaya geldi.

Bir ip uçu olması açısından en son elde ettiğimiz integral sabitinin değeri her zaman sıfırdır. Buna göre yukarıda elde ettiğimiz en son integral sabiti olan d'nin değeri sıfıra eşittir.

1² + 3² + 5² + ... + (2n - 1)² = n . (2n - 1) . (2n + 1) / 3

1⁴ + 2⁴ + 3⁴ + ... + n⁴ = n . (n + 1) . (2n + 1) . (3n² + 3n - 1) / 30

Yukarıdaki eşitliklerin ispatını da gösterdiğimiz yolu kullanarak siz yapın isterseniz.