Dairenin Alanı Formülü

Çember Nedir?

Düzlemde sabit bir noktadan eşit uzaklıktaki noktalar kümesine çember denir. Sabit noktaya çemberin merkezi, çemberin merkezi ile çember arasındaki uzaklığa ise çemberin yarıçapı denir. Yukarıdaki şekildeki çemberde O noktası çemberin merkezi r'ler ise çemberin yarıçaplarıdır.

Çemberin Çevresi

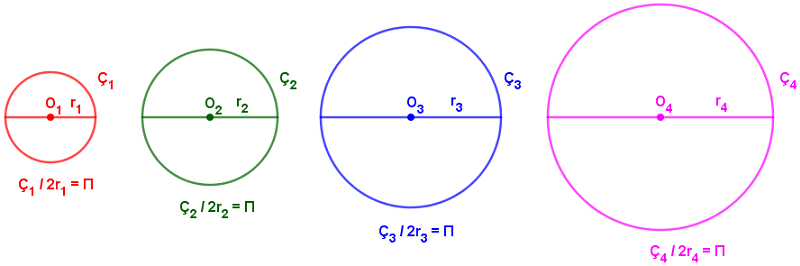
Herhangi bir çemberin çevre ve çap uzunluklarını ölçer ve birbirine oranlarsak çevrenin çapın üç katından biraz daha uzun olduğunu görürüz. Çember ve çember şeklindeki bütün cisimler için geçerli olan bu oran Yunan alfabesindeki π (pi) harfiyle gösterilen ve pi sayısı denilen irrasyonel sabit bir sayıdır.

Çevre / Çap = Sabit

Ç / 2r = π

Ç = 2πr olur.

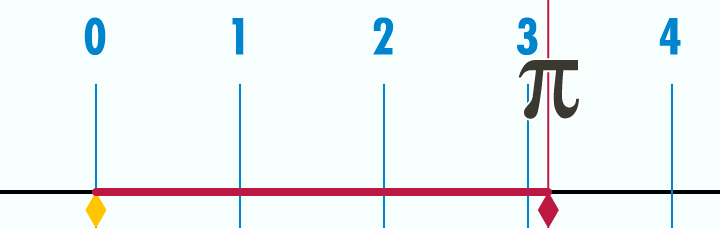
Tarih boyunca insanlar π sayısı için çeşitli yaklaşık değerler kullanmışlardır. Kudüs'teki Süleyman Tapınağı'nı inşa eden İbraniler π sayısını 3 olarak almışlardır. Babilliler M.Ö. 1900-1600 arası π'yi 25/8 (3,125), Eski Mısırlılar ise M.Ö. 1650'ler de 256/81 (3,1605) olarak tahmin ettiler. Eski Yunan matematikçi ve mühendis Arşimet (M.Ö. 287-212) bir çemberin içine ve dışına düzgün çokgenler çizerek (96 tane düzgün çokgen çizmiştir) π'nin 223/71 (3,1408) ile 220/70 (3,1429) arasında olduğunu ispatladı. π'nin ilk birkaç ondalık basamağı 3.1415926535 şeklindedir ve uygulamada 3,14 olarak almak çoğu zaman yeterlidir.

Örnek

Yarıçapı 5 cm olan bir çemberin çevresinin uzunluğu ne kadardır? (π = 3,14)

Cevap

Ç = 2πr

Ç = 2x3,14x5

Ç = 31,4 cm olur.

Daire Nedir?

Çemberin içinde kalan bölgeye daire denir. Yukarıdaki O merkezli r yarıçaplı çemberde yeşil bölge çemberin dairesi veya alanıdır.

Dairenin Alanı = Pi sayısı x Yarıçap²

A = πr² olur.

Dairenin Alanı Nasıl Bulunur? (Dairenin Alanı Nasıl Hesaplanır?)

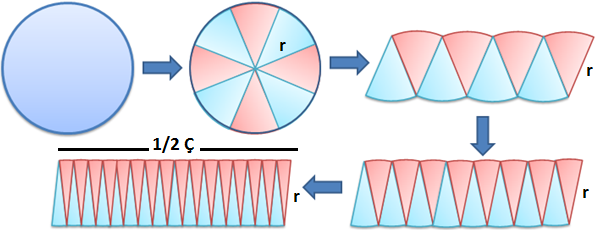
Yukarıdaki daireyi şekildeki gibi merkezinden geçen doğru parçalarıyla dilimlere ayıralım ve bu dilimleri yan yana dizelim. Daireyi daha da çok dilime bölmeye devam ettiğimizde her dilim giderek incelecek ve sonunda neredeyse birer çizgi boyutuna gelecektir. Birer çizgi boyutuna gelen sonsuz incelikteki bu daire dilimlerinin yanyana dizilmesiyle oluşan şekil artık bir diktörgene benzer.

Oluşan bu dikdörtgenin yüksekliği dairenin yarıçapı olan r kadar, genişliği ise dairenin çevresinin yarısı olan Ç/2 kadardır. Çünkü dairenin çevresi dikdörgenin alt ve üst kenarları arasında eşit olarak bölünmüştür.

Diktörtgenin Alanı = Genişlik x Yükseklik

A = a.h

a = Ç/2

h = r

A = Ç/2.r

(Ç = 2πr)

A = 2πr/2.r

A = πr.r

A = πr² olur.

Örnek

Yarıçapı 5 cm olan bir dairenin alanı ne kadardır? (π = 3,14)

Cevap

A = πr²

A = 3,14x5²

A = 78,5 cm² olur.