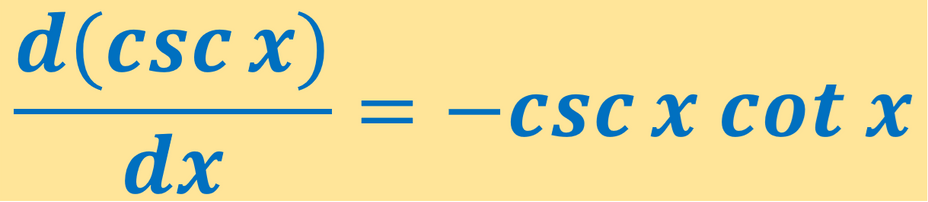¿ Cuál es la Derivada de Csc x ?
La derivada de csc x es -csc x.cot x.
(csc x)′=−csc x.cot x
dxd(csc x)=−csc x.cot x
Prueba de la Derivada de Csc x
Método 1
f′ (x)=h→0limhf (x+h)−f (x)
(csc x)′=h→0limhcsc (x+h)−csc x
csc x=sin x1
(csc x)′=h→0limhsin (x+h)1−sin x1
(csc x)′=h→0limhsin x.sin (x+h)sin x−sin (x+h)
(csc x)′=h→0lim [h1.sin x.sin (x+h)sin x−sin (x+h)]
(csc x)′=h→0limh.sin x.sin (x+h)sin x−sin (x+h)
sin p−sin q=2.sin 2p−q.cos 2p+q
(csc x)′=h→0limh.sin x.sin (x+h)2.sin 2x−(x+h).cos 2x+x+h
(csc x)′=h→0limh.sin x.sin (x+h)2.sin 2x−x−h.cos 22x+h
(csc x)′=h→0limh.sin x.sin (x+h)2.sin 2−h.cos 22x+h
sin (−x)=−sin x
(csc x)′=h→0limh.sin x.sin (x+h)2.−sin 2h.cos 22x+h
(csc x)′=h→0limh.sin x.sin (x+h)2.−sin 2h.cos 22.(x+2h)
(csc x)′=h→0limh.sin x.sin (x+h)2.−sin 2h.cos (x+2h)
(csc x)′=h→0lim21.h.sin x.sin (x+h)−sin 2h.cos (x+2h)
(csc x)′=h→0lim2h.sin x.sin (x+h)−sin 2h.cos (x+2h)
(csc x)′=h→0lim [2h−sin 2h.sin x.sin (x+h)cos (x+2h)]
(csc x)′=h→0lim2h−sin 2h.h→0limsin x.sin (x+h)cos (x+2h)
h→0 (2h=h)
(csc x)′=h→0limh−sin h.h→0limsin x.sin (x+h)cos (x+h)
(csc x)′=−h→0limhsin h.h→0limsin x.sin (x+h)cos (x+h)
t→0limtsin t=1
(csc x)′=−1.sin x.sin (x+0)cos (x+0)
(csc x)′=−sin x.sin (x+0)cos (x+0)
(csc x)′=−sin x.sin xcos x
(csc x)′=−sin x.sin x1.cos x
(csc x)′=−sin x1.sin xcos x
sin x1=csc x sin xcos x=cot x
(csc x)′=−csc x.cot x
Método 2
csc x=sin x1
(csc x)′=(sin x1)′
(vu)′=v2u′.v−v′.u
(csc x)′=sin2 x(1)′.sin x−(sin x)′.1
(sin x)′=cos x
(csc x)′=sin2 x0.sin x−cos x.1
(csc x)′=sin2 x0−cos x
(csc x)′=sin2 x−cos x
(csc x)′=−sin2 xcos x
(csc x)′=−sin x.sin x1.cos x
(csc x)′=−sin x1.sin xcos x
(csc x)′=−csc x.cot x
Método 3
csc x=sin x1
csc x=sin−1 x
(csc x)′=(sin−1 x)′
(un)′=n.un−1.u′
(csc x)′=−1.sin−1−1 x.(sin x)′
(csc x)′=−1.sin−2 x.cos x
(csc x)′=−sin−2 x.cos x
(csc x)′=−sin2 x1.cos x
(csc x)′=−sin2 xcos x
(csc x)′=−sin x.sin x1.cos x
(csc x)′=−sin x1.sin xcos x
(csc x)′=−csc x.cot x
Published Date:
November 09, 2024
Updated Date:
April 13, 2025