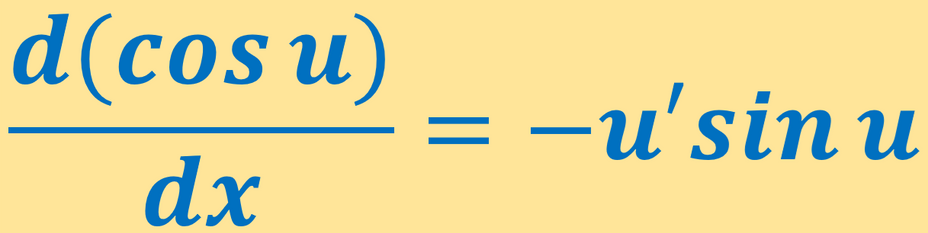What is the Derivative of Cos u ?
The derivative of cos u is -u'.sin u.
(cos u)′=−u′.sin u
dxd(cos u)=−u′.sin u
Proof of the Derivative of Cos u
Way 1
f′ (x)=h→0limhf (x+h)−f (x)
[cos u(x)]′=h→0limhcos u(x+h)−cos u(x)
cos p−cos q=−2.sin 2p+q.sin 2p−q
[cos u(x)]′=h→0limh−2.sin 2u(x+h)+u(x).sin 2u(x+h)−u(x)
[cos u(x)]′=h→0limh.21−sin 2u(x+h)+u(x).sin 2u(x+h)−u(x)
[cos u(x)]′=h→0limh.21.[u(x+h)−u(x)]−[u(x+h)−u(x)].sin 2u(x+h)+u(x).sin 2u(x+h)−u(x)
[cos u(x)]′=h→0limh.2u(x+h)−u(x)−[u(x+h)−u(x)].sin 2u(x+h)+u(x).sin 2u(x+h)−u(x)
[cos u(x)]′=−h→0limh.2u(x+h)−u(x)[u(x+h)−u(x)].sin 2u(x+h)+u(x).sin 2u(x+h)−u(x)
[cos u(x)]′=−h→0lim [hu(x+h)−u(x).2u(x+h)−u(x)sin 2u(x+h)−u(x).sin 2u(x+h)+u(x)]
[cos u(x)]′=−h→0limhu(x+h)−u(x).h→0lim2u(x+h)−u(x)sin 2u(x+h)−u(x).h→0limsin 2u(x+h)+u(x)
h→0 [2u(x+h)−u(x)=h]
[cos u(x)]′=−h→0limhu(x+h)−u(x).h→0limhsin h.h→0limsin 2u(x+h)+u(x)
t→0limtsin t=1
[cos u(x)]′=−u′(x).1.sin 2u(x+0)+u(x)
[cos u(x)]′=−u′(x).1.sin 2u(x)+u(x)
[cos u(x)]′=−u′(x).1.sin 22.u(x)
[cos u(x)]′=−u′(x).1.sin u(x)
[cos u(x)]′=−u′(x).sin u(x)
u(x)=u
u′(x)=u′
(cos u)′=−u′.sin u
Way 2
sin u(x)=u(x)−3![u(x)]3+5![u(x)]5−7![u(x)]7+9![u(x)]9−...
cos u(x)=1−2![u(x)]2+4![u(x)]4−6![u(x)]6+8![u(x)]8−...
u(x)=u
u′(x)=u′
cos u=1−2!u2+4!u4−6!u6+8!u8−...
(cos u)′=(1−2!u2+4!u4−6!u6+8!u8−...)′
(cos u)′=(1)′−(2!u2)′+(4!u4)′−(6!u6)′+(8!u8)′−...
(cos u)′=(1)′−2!(u2)′+4!(u4)′−6!(u6)′+8!(u8)′−...
(cos u)′=0−2!2.u.u′+4!4.u3.u′−6!6.u5.u′+8!8.u7.u′−...
(cos u)′=−2!2.u.u′+4!4.u3.u′−6!6.u5.u′+8!8.u7.u′−...
(cos u)′=−2.1!2.u.u′+4.3!4.u3.u′−6.5!6.u5.u′+8.7!8.u7.u′−...
(cos u)′=−1!u.u′+3!u3.u′−5!u5.u′+7!u7.u′−...
(cos u)′=−1u.u′+3!u3.u′−5!u5.u′+7!u7.u′−...
(cos u)′=−u.u′+3!u3.u′−5!u5.u′+7!u7.u′−...
(cos u)′=−u′.(u−3!u3+5!u5−7!u7+...)
(cos u)′=−u′.sin u
Question
f(x)=cos (−2x3+4x)⇒f′(x)= ?
Answer
(cos u)′=−u′.sin u
[cos (−2x3+4x)]′=−(−2x3+4x)′.sin (−2x3+4x)
[cos (−2x3+4x)]′=−(−2.3.x2+4).sin (−2x3+4x)
[cos (−2x3+4x)]′=−(−6x2+4).sin (−2x3+4x)
[cos (−2x3+4x)]′=(6x2−4).sin (−2x3+4x)
Published Date:
June 14, 2024
Updated Date:
April 16, 2025