Derivative of Cot u

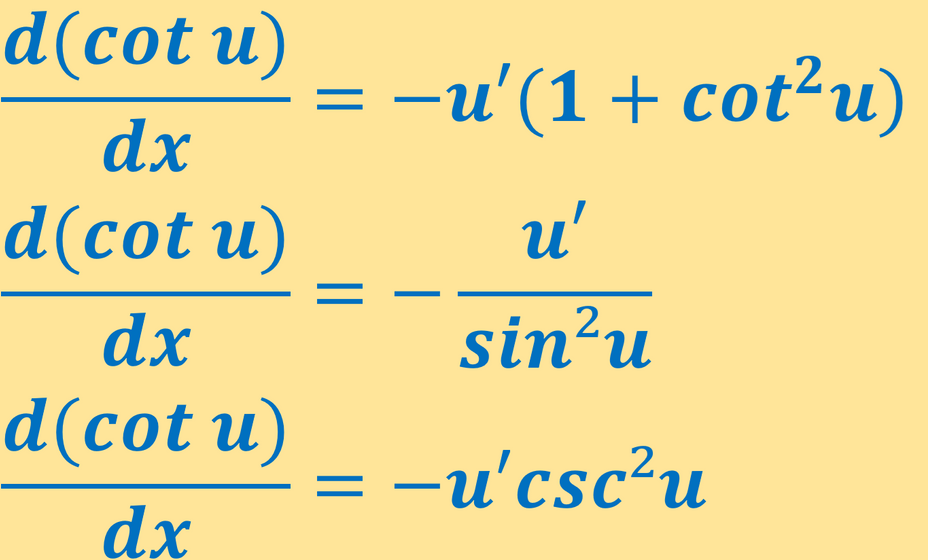
What is the Derivative of Cot u ?

The derivative of cot u is -u'.(1+cot² u).

$(cotu{)}^{\prime }=-u^{\prime }.(1+co{t}^{2}u)$

$\frac{d}{dx}(cotu)=-u^{\prime }.(1+co{t}^{2}u)$

Proof of the Derivative of Cot u

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{cotu(x+h)-cotu(x)}{h}$

$\boxed{cotx=\frac{cosx}{sinx}}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{\frac{cosu(x+h)}{sinu(x+h)}-\frac{cosu(x)}{sinu(x)}}{h}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{\frac{sinu(x).cosu(x+h)-cosu(x).sinu(x+h)}{sinu(x).sinu(x+h)}}{h}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{sinu(x).cosu(x+h)-cosu(x).sinu(x+h)}{h.sinu(x).sinu(x+h)}$

$\boxed{sinp.cosq-cosp.sinq=sin(p-q)}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{sin[u(x)-u(x+h)]}{h.sinu(x).sinu(x+h)}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{sin\{-[u(x+h)-u(x)]\}}{h.sinu(x).sinu(x+h)}$

$\boxed{sin(-x)=-sinx}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{-sin[u(x+h)-u(x)]}{h.sinu(x).sinu(x+h)}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{-[u(x+h)-u(x)].sin[u(x+h)-u(x)]}{[u(x+h)-u(x)].h.sinu(x).sinu(x+h)}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\{\frac{-[u(x+h)-u(x)]}{h}.\frac{sin[u(x+h)-u(x)]}{u(x+h)-u(x)}.\frac{1}{sinu(x).sinu(x+h)}\}$

$[cotu(x){]}^{\prime }=\underset{h\to 0}{\lim }\frac{-[u(x+h)-u(x)]}{h}.\underset{h\to 0}{\lim }\frac{sin[u(x+h)-u(x)]}{u(x+h)-u(x)}.\underset{h\to 0}{\lim }\frac{1}{sinu(x).sinu(x+h)}$

$[cotu(x){]}^{\prime }=-\underset{h\to 0}{\lim }\frac{u(x+h)-u(x)}{h}.\underset{h\to 0}{\lim }\frac{sin[u(x+h)-u(x)]}{u(x+h)-u(x)}.\underset{h\to 0}{\lim }\frac{1}{sinu(x).sinu(x+h)}$

$h\to 0[u(x+h)-u(x)=h]$

$[cotu(x){]}^{\prime }=-\underset{h\to 0}{\lim }\frac{u(x+h)-u(x)}{h}.\underset{h\to 0}{\lim }\frac{sinh}{h}.\underset{h\to 0}{\lim }\frac{1}{sinu(x).sinu(x+h)}$

$\boxed{\underset{t\to 0}{\lim }\frac{sint}{t}=1}$

$[cotu(x){]}^{\prime }=-u^{\prime }(x).1.\frac{1}{sinu(x).sinu(x+0)}$

$[cotu(x){]}^{\prime }=-u^{\prime }(x).1.\frac{1}{sinu(x).sinu(x)}$

$[cotu(x){]}^{\prime }=-\frac{u^{\prime }(x).1.1}{si{n}^{2}u(x)}$

$[cotu(x){]}^{\prime }=-\frac{u^{\prime }(x)}{si{n}^{2}u(x)}$

$u(x)=u$

$u^{\prime }(x)=u^{\prime }$

$(cotu{)}^{\prime }=-\frac{u^{\prime }}{si{n}^{2}u}$

$(cotu{)}^{\prime }=-u^{\prime }.\frac{1}{si{n}^{2}u}$

$(cotu{)}^{\prime }=-u^{\prime }.(\frac{1}{sinu}{)}^2$

$\boxed{\frac{1}{sinx}=cscx}$

$(cotu{)}^{\prime }=-u^{\prime }.cs{c}^{2}u$

$(cotu{)}^{\prime }=-u^{\prime }.\frac{1}{si{n}^{2}u}$

$\boxed{1=si{n}^{2}x+co{s}^{2}x}$

$(cotu{)}^{\prime }=-u^{\prime }.(\frac{si{n}^{2}u+co{s}^{2}u}{si{n}^{2}u})$

$(cotu{)}^{\prime }=-u^{\prime }.(\frac{\cancel{si{n}^{2}u}}{\cancel{si{n}^{2}u}}+\frac{co{s}^{2}u}{si{n}^{2}u})$

$(cotu{)}^{\prime }=-u^{\prime }.[1+(\frac{cosu}{sinu}{)}^2]$

$(cotu{)}^{\prime }=-u^{\prime }.(1+co{t}^{2}u)$

$(cotu{)}^{\prime }=-u^{\prime }.(1+co{t}^{2}u)=-\frac{u^{\prime }}{si{n}^{2}u}=-u^{\prime }.cs{c}^{2}u$

Question

$f(x)=cot3x\Rightarrow f^{\prime }(x)=?$

Answer

$(cotu{)}^{\prime }=-u^{\prime }.(1+co{t}^{2}u)$

$(cot3x{)}^{\prime }=-(3x{)}^{\prime }.(1+co{t}^{2}3x)$

$(cot3x{)}^{\prime }=-3.(1+co{t}^{2}3x)$

$(cot3x{)}^{\prime }=-3.1-3.co{t}^{2}3x$

$(cot3x{)}^{\prime }=-3-3.co{t}^{2}3x$