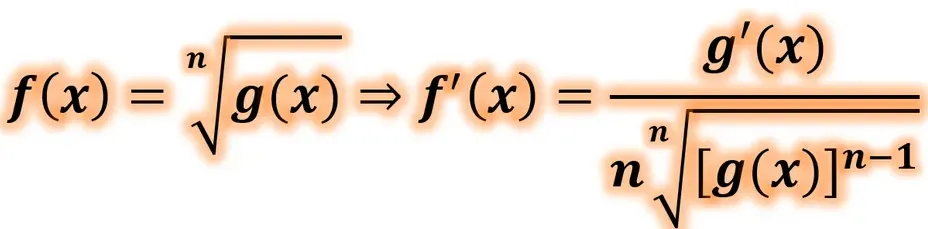n > 1 : n ∈ N⁺, g(x) > 0; f(x) = ⁿ√g(x) ⇒ f'(x) = g'(x)/nⁿ√[g(x)]ⁿ⁻¹.
poof of derivative of radical functions f ( x ) = n g ( x ) ⇒ f ′ ( x ) = n n ( g ( x ) ) n − 1 g ′ ( x ) ( n > 1 : n ∈ N + , g ( x ) > 0 ) . We can prove why the derivative of n g ( x ) is equal to n n ( g ( x ) ) n − 1 g ′ ( x ) in several ways, some of which we will show below.
Way 1 f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) ( n g ( x ) ) ′ = h → 0 lim h n g ( x + h ) − n g ( x )
( n g ( x ) ) ′ = h → 0 lim h n g ( x + h ) − n g ( x ) . n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1
( n g ( x ) ) ′ = h → 0 lim h . ( n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 ) ( n g ( x + h ) − n g ( x ) ) . ( n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 )
a n − b n = ( a − b ) . ( a n − 1 + a n − 2 . b + a n − 3 . b 2 + ... + a 2 . b n − 3 + a . b n − 2 + b n − 1 )
( n g ( x ) ) ′ = h → 0 lim h . ( n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 ) n [ g ( x + h ) ] n − n [ g ( x ) ] n
( n g ( x ) ) ′ = h → 0 lim h . ( n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 ) g ( x + h ) − g ( x )
( g ( x ) ) ′ = h → 0 lim h g ( x + h ) − g ( x ) . n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = h → 0 lim h g ( x + h ) − g ( x ) . h → 0 lim n [ g ( x + h ) ] n − 1 + n [ g ( x + h ) ] n − 2 . n g ( x ) + n [ g ( x + h ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = g ′ ( x ) . n [ g ( x + 0 ) ] n − 1 + n [ g ( x + 0 ) ] n − 2 . n g ( x ) + n [ g ( x + 0 ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = g ′ ( x ) . n [ g ( x ) ] n − 1 + n [ g ( x ) ] n − 2 . n g ( x ) + n [ g ( x ) ] n − 3 . n [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = g ′ ( x ) . n [ g ( x ) ] n − 1 + n [ g ( x ) ] n − 2 . g ( x ) + n [ g ( x ) ] n − 3 . [ g ( x ) ] 2 + ... + n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = g ′ ( x ) . n [ g ( x ) ] n − 1 + n [ g ( x ) ] n − 2 + 1 + n [ g ( x ) ] n − 3 + 2 + ... + n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = g ′ ( x ) . n tane n [ g ( x ) ] n − 1 + n [ g ( x ) ] n − 1 + n [ g ( x ) ] n − 1 + ... + n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = g ′ ( x ) . n . n [ g ( x ) ] n − 1 1
( g ( x ) ) ′ = n . n [ g ( x ) ] n − 1 g ′ ( x ) .1
( g ( x ) ) ′ = n . n ( g ( x ) ) n − 1 g ′ ( x )
Way 2 f ( x ) = n g ( x )
[ f ( x ) ] n = ( n g ( x ) ) n
[ f ( x ) ] n = n [ g ( x ) ] n
[ f ( x ) ] n = g ( x )
{[ f ( x ) ] n } ′ = [ g ( x ) ] ′
{[ f ( x ) ] n } ′ = g ′ ( x )
f ( x ) = [ g ( x ) ] n ⇒ f ′ ( x ) = n . [ g ( x ) ] n − 1 . g ′ ( x )
n . [ f ( x ) ] n − 1 . f ′ ( x ) = g ′ ( x )
f ′ ( x ) = n . [ f ( x ) ] n − 1 g ′ ( x )
f ′ ( x ) = n . ( n g ( x ) ) n − 1 g ′ ( x )
f ′ ( x ) = n . n [ g ( x ) ] n − 1 g ′ ( x )
Way 3 n g ( x ) = [ g ( x ) ] n 1
l n n g ( x ) = l n [ g ( x ) ] n 1
l n n g ( x ) = n 1 . [ l n g ( x )]
( l n n g ( x ) ) ′ = { n 1 . [ l n g ( x )] } ′
( l n n g ( x ) ) ′ = n 1 . [ l n g ( x ) ] ′
f ( x ) = l n g ( x ) ⇒ f ′ ( x ) = g ( x ) g ′ ( x )
n g ( x ) ( n g ( x ) ) ′ = n 1 . g ( x ) g ′ ( x )
n g ( x ) ( n g ( x ) ) ′ = n . g ( x ) 1. g ′ ( x )
n g ( x ) ( n g ( x ) ) ′ = n . g ( x ) g ′ ( x )
( n g ( x ) ) ′ = n g ( x ) . n . g ( x ) g ′ ( x )
( n g ( x ) ) ′ = n . g ( x ) n g ( x ) . g ′ ( x )
( n g ( x ) ) ′ = n . n [ g ( x ) ] n n g ( x ) . g ′ ( x )
( n g ( x ) ) ′ = n . n [ g ( x ) ] n − 1 . g ( x ) n g ( x ) . g ′ ( x )
( n g ( x ) ) ′ = n . n [ g ( x ) ] n − 1 . n g ( x ) n g ( x ) . g ′ ( x )
( g ( x ) ) ′ = n . n [ g ( x ) ] n − 1 g ′ ( x )