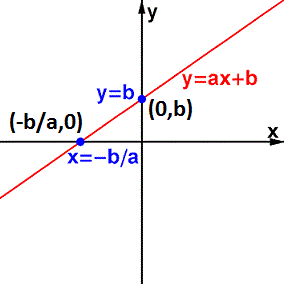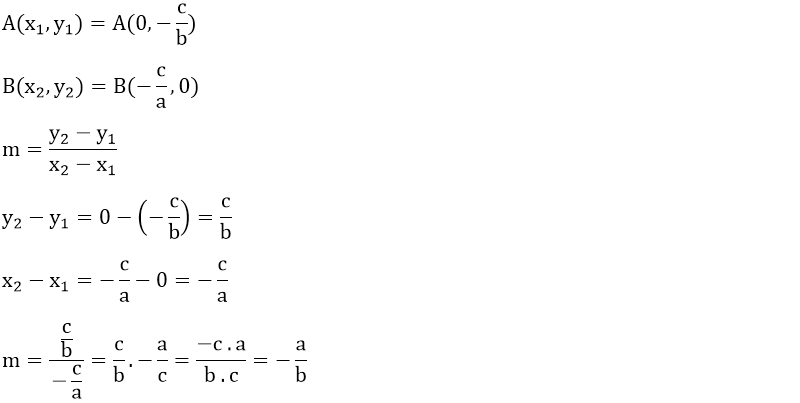Doğrunun Eğimi
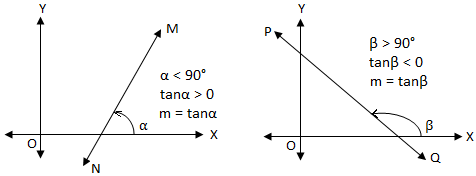
Eğim ve Eğim Açısı Nedir ? Bir doğrunun x ekseni ile pozitif (saat yönünün tersi) yönde yaptığı açıya o doğrunun eğim açısı denir. Eğim açısının tanjantına ise

Pow
@powEğim ve Eğim Açısı Nedir ?
Bir doğrunun x ekseni ile pozitif (saat yönünün tersi) yönde yaptığı açıya o doğrunun eğim açısı denir. Eğim açısının tanjantına ise o doğrunun eğimi denir. Eğim "m" harfi ile gösterilir. Matematikte bir doğrunun eğimi o doğrunun dikliğini, eğimliliğini ifade eder. Daha büyük bir eğim, daha dik bir doğru demektir.
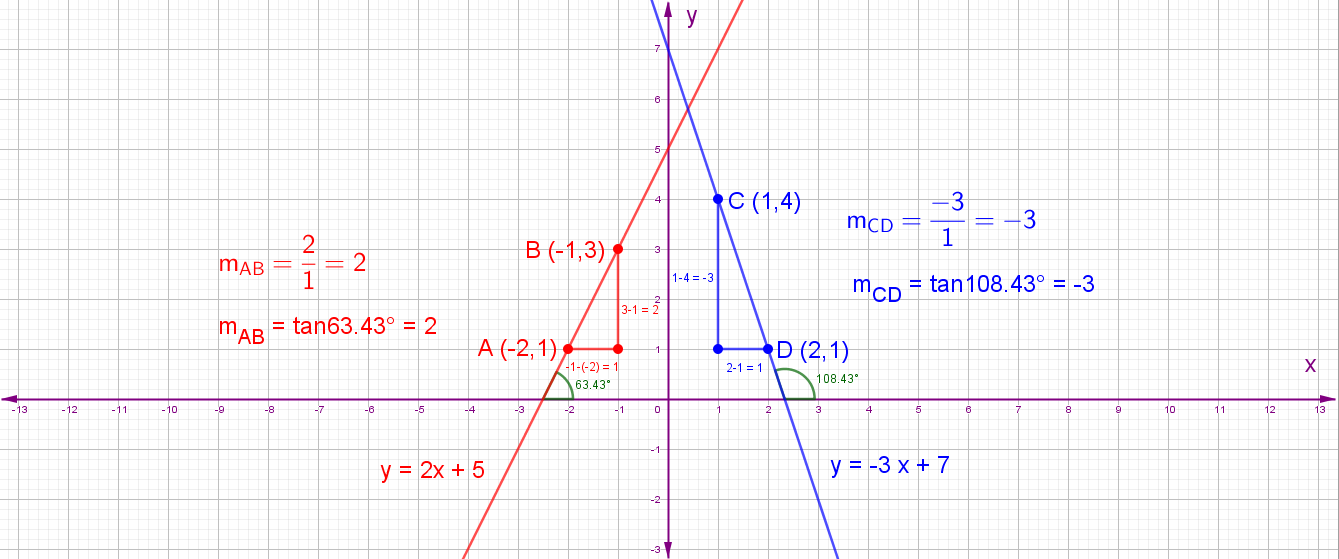
Eğer verilen doğrunun eğiminin açısı dar bir açısı ise (0 < α < 90), tanα > 0 olacağından eğim pozitif (+) olur. Eğer verilen doğrunun eğiminin açısı geniş bir açısı ise (90 < β < 180), tanβ < 0 olacağından eğim negatif (-) olur.
1. İki Noktası Bilinen Doğrunun Eğimi
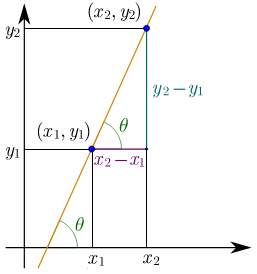
Eğim, bir doğrunun herhangi iki noktası arasında dikey değişimdeki büyüklüğün yatay değişimdeki büyüklüğe oranı olarak da tanımlanabilir.
Yukarıdaki şekildeki doğrunun eğimi;
Örnek
A (-3, 7) ve B (2, 4) noktalarından geçen doğrunun eğimi nedir ?
Cevap
m = Δx/Δy
Δx = 4 - 7 = -3
Δy = 2 - (-3) = 2 + 3 = 5
m = -3/5 = -0,6 olur.
2. y = ax + b Şeklindeki Doğrunun Eğimi
y = ax + b şeklindeki bir doğru analitik düzlemde x eksenini -b/a ve y eksenini de b noktalarından kesecek şekilde geçer. y = ax + b şeklindeki bir doğrunun eğimi ise x'in önündeki katsayı olan "a"ya eşittir.
a > 0 ise doğrunun eğimi pozitif (+) ve x ekseni ile yaptığı açı da dar bir açı olur. a < 0 ise doğrunun eğimi negatif (-) ve x ekseni ile yaptığı açı da geniş bir açı olur.
İspat
3. ax + by + c = 0 Şeklindeki Doğrunun Eğimi
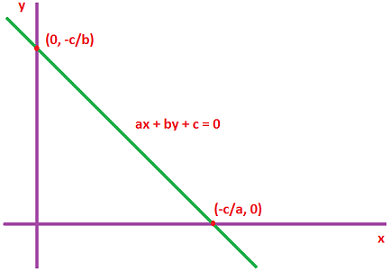
ax + by + c = 0 şeklindeki bir doğru analitik düzlemde x eksenini -c/a ve y eksenini de -c/b noktalarından kesecek şekilde geçer. ax + by + c = 0 şeklindeki bir doğrunun eğimi ise "-a/b"ye eşittir.
-a/b > 0 ise doğrunun eğimi pozitif (+) ve x ekseni ile yaptığı açı da dar bir açı olur. -a/b < 0 ise doğrunun eğimi negatif (-) ve x ekseni ile yaptığı açı da geniş bir açı olur.
ax + by + c = 0 şeklindeki bir doğrunun eğimini pratik yoldan aşağıdaki şekildeki gibi bulabiliriz. y'yi yalnız bıraktığımızda x'in önündeki katsayı doğrunun eğimini verir.
ax + by + c = 0
by = -ax - c
y = -a/b.x - c/b
m = -a/b olur.
İspat
Published Date:
May 12, 2021
Updated Date:
December 12, 2023