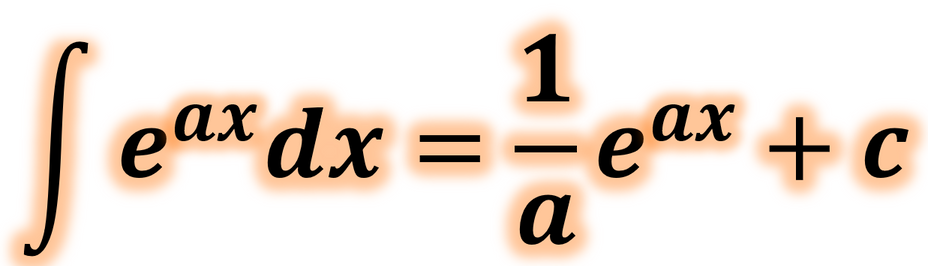integral of e to the ax

what is the integral of e to the ax?

$\int e^{ax}dx=\frac{e^{ax}}{a}+c(a>0)$.

proof of the integral of e to the ax

We can prove why the integral of $e^{ax}$ is equal to $\frac{e^{ax}}{a}$ in several ways, some of which we will show below.

way 1

$\int e^{ax}dx=?$

let $ax=u$.

$d(ax)=du$ (we take the differential of both sides of the equation)

$(ax{)}^{\prime }dx=du$

$adx=du$

$dx=\frac{du}{a}$

$\int e^{ax}dx=\int e^u.\frac{du}{a}$

$\int e^{ax}dx=\int \frac{e^{u}du}{a}$

$\int e^{ax}dx=\frac{1}{a}.\int e^{u}du$

$\int e^{x}dx=e^x+c\Rightarrow \int e^{u}du=e^u+c$.

$\int e^{ax}dx=\frac{e^u}{a}+c$

way 2

$\int e^{ax}dx=?$

let $e^{ax}=u$.

$d(e^{ax})=du$ (we take the differential of both sides of the equation)

$(e^{ax}{)}^{\prime }dx=du$

$\boxed{f(x)=e^{ax}\Rightarrow f^{\prime }(x)=a.e^{ax}}$

$a.e^{ax}dx=du$

$e^{ax}dx=\frac{du}{a}$

$\int e^{ax}dx=\int \frac{du}{a}$

$\int e^{ax}dx=\frac{1}{a}.\int du$

$\int dx=x+c\Rightarrow \int du=u+c$.

$\int e^{ax}dx=\frac{u}{a}+c$

$\int e^{ax}dx=\frac{e^{ax}}{a}+c$

way 3

$\int e^{ax}dx=?$

let $e^{ax}=u$.

$ln{e}^{ax}=lnu$

$ax.lne=lnu$

$ax.1=lnu$

$ax=lnu$

$d(ax)=d(lnu)$ (we take the differential of both sides of the equation)

$(ax{)}^{\prime }dx=(lnu{)}^{\prime }du$

$\boxed{f(x)=lng(x)\Rightarrow f^{\prime }(x)=\frac{g^{\prime }(x)}{g(x)}}$

$a.dx=\frac{u^{\prime }}{u}.du$

$a.dx=\frac{1}{u}.du$

$a.dx=\frac{1.du}{u}$

$a.dx=\frac{du}{u}$

$dx=\frac{du}{a.u}$

$\int e^{ax}dx=\int \cancel{u}.\frac{du}{a.\cancel{u}}$

$\int e^{ax}dx=\int \frac{du}{a}$

$\int e^{ax}dx=\frac{1}{a}.\int du$

$\int dx=x+c\Rightarrow \int du=u+c$.

$\int e^{ax}dx=\frac{u}{a}+c$

$\int e^{ax}dx=\frac{e^{ax}}{a}+c$

way 4

by using the infinite series expansion of the $e^{ax}$ function, we can prove that the integral of $e^{ax}$ is equal to $\frac{e^{ax}}{a}$. The infinite series expansion of the $e^{ax}$ function is as follows

$e^{ax}=1+a.x+\frac{(a.x{)}^2}{2!}+\frac{(a.x{)}^3}{3!}+\frac{(a.x{)}^4}{4!}+...$

$\int e^{ax}dx=\int (1+a.x+\frac{(a.x{)}^2}{2!}+\frac{(a.x{)}^3}{3!}+\frac{(a.x{)}^4}{4!}+...)dx$ (we take the integral of both sides of the equation)

$\int e^{ax}dx=\int (1+a.x+\frac{a^2.x^2}{2!}+\frac{a^3.x^3}{3!}+\frac{a^4.x^4}{4!}+...)dx$

$\boxed{\int x^{n}dx=\frac{x^{n+1}}{n+1}+c}$

$\int e^{ax}dx=x+\frac{a.x^2}{2}+\frac{a^2.x^3}{3.2!}+\frac{a^3.x^4}{4.3!}+\frac{a^4.x^5}{5.4!}+...+c$

$\int e^{ax}dx=c+x+\frac{a.x^2}{2!}+\frac{a^2.x^3}{3!}+\frac{a^3.x^4}{4!}+\frac{a^4.x^5}{5!}+...$

$a.\int e^{ax}dx=a.(c+x+\frac{a.x^2}{2!}+\frac{a^2.x^3}{3!}+\frac{a^3.x^4}{4!}+\frac{a^4.x^5}{5!}+...)$ (sides of the equation by a)

$a.\int e^{ax}dx=a.c+a.x+\frac{a^2.x^2}{2!}+\frac{a^3.x^3}{3!}+\frac{a^4.x^4}{4!}+\frac{a^5.x^5}{5!}+...$

$a.\int e^{ax}dx=1+a.x+\frac{(a.x{)}^2}{2!}+\frac{(a.x{)}^3}{3!}+\frac{(a.x{)}^4}{4!}+\frac{(a.x{)}^5}{5!}+...$ (a.c = 1)

$a.\int e^{ax}dx=e^{ax}$

$\int e^{ax}dx=\frac{e^{ax}}{a}$