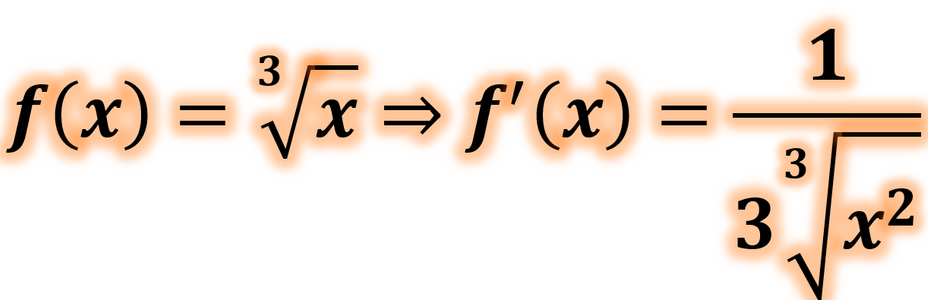
küpkök x'in türevi nedir ?
f(x)=3x⇒f′(x)=33x21
küpkök x'in türevinin ispatı
1. Yol
f′(x)=h→0limhf(x+h)−f(x)
(3x)′=h→0limh3x+h−3x
(3x)′=h→0limh3x+h−3x.(3x+h)2+3x+h.3x+(3x)2(3x+h)2+3x+h.3x+(3x)2
(3x)′=h→0limh3x+h−3x.3(x+h)2+3(x+h).x+3x23(x+h)2+3(x+h).x+3x2
(3x)′=h→0limh.(3(x+h)2+3(x+h).x+3x2)(3x+h−3x).(3(x+h)2+3(x+h).x+3x2)
a3−b3=(a−b).(a2+ab+b2)
(3x)′=h→0limh.(3(x+h)2+3(x+h).x+3x2)3(x+h)3−3x3
(3x)′=h→0limh.(3x2+2.x.h+h2+3x2+x.h+3x2)x+h−x
(3x)′=h→0limh.(3x2+2.x.h+h2+3x2+x.h+3x2)h
(3x)′=h→0lim3x2+2.x.h+h2+3x2+x.h+3x21
(3x)′=3x2+2.x.0+02+3x2+x.0+3x21
(3x)′=3x2+0+0+3x2+0+3x21
(3x)′=3x2+3x2+3x21
(3x)′=3.3x21
2. Yol
f(x)=3x
[f(x)]3=(3x)3
[f(x)]3=3x3
[f(x)]3=x
{[f(x)]3}′=(x)′
f(x)=[g(x)]n⇒f′(x)=n.[g(x)]n−1.g′(x)
3.[f(x)]3−1.f′(x)=1
3.[f(x)]2.f′(x)=1
f′(x)=3.[f(x)]21
f′(x)=3.(3x)21
f′(x)=3.3x21
3. Yol
3x=x31
ln3x=lnx31
ln3x=31.lnx
(ln3x)′=(31.lnx)′
(ln3x)′=31.(lnx)′
f(x)=lng(x)⇒f′(x)=g(x)g′(x)
3x(3x)′=31.x(x)′
3x(3x)′=31.x1
3x(3x)′=3.x1.1
3x(3x)′=3.x1
(3x)′=3x.3x1
(3x)′=3.x3x.1
(3x)′=3.x3x
(3x)′=3.3x33x
(3x)′=3.3x2.x3x
(3x)′=3.3x2.3x3x
(3x)′=3.3x21