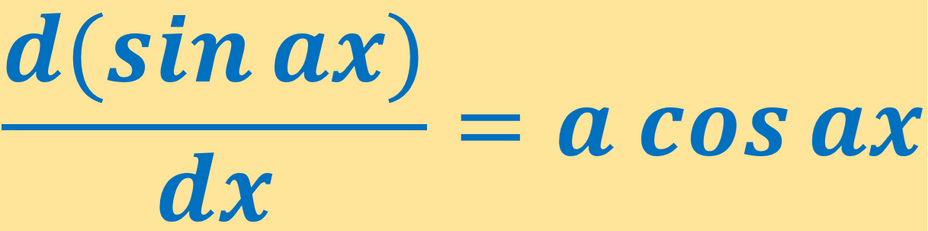Sin ax'in Türevi Nedir ?
Sin ax'in türevi a.cos ax'tir.
(sin ax)′=a.cos ax
dxd(sin ax)=a.cos ax
Sin ax'in Türevinin İspatı
1. Yol
f′ (x)=h→0limhf (x+h)−f (x)
(sin ax)′=h→0limhsin a(x+h)−sin ax
(sin ax)′=h→0limhsin (ax+ah)−sin ax
sin (p+q)=sin p.cos q+cos p.sin q
(sin ax)′=h→0limhsin ax.cos ah+cos ax.sin ah−sin ax
(sin ax)′=h→0limhsin ax.cos ah−sin ax+cos ax.sin ah
(sin ax)′=h→0limhsin ax.(cos ah−1)+cos ax.sin ah
(sin ax)′=h→0lima.ha.[sin ax.(cos ah−1)+cos ax.sin ah]
(sin ax)′=a.h→0limahsin ax.(cos ah−1)+cos ax.sin ah
(sin ax)′=a.h→0lim[ahsin ax.(cos ah−1)+ahcos ax.sin ah]
(sin ax)′=a.h→0limahsin ax.(cos ah−1)+a.h→0limahcos ax.sin ah
(sin ax)′=a.sin ax.h→0limahcos ah−1+a.cos ax.h→0limahsin ah
h→0 (ah=h)
(sin ax)′=a.sin ax.h→0limhcos h−1+a.cos ax.h→0limhsin h
t→0limtsin t=1 t→0limtcos t−1=0
(sin ax)′=a.sin ax.0+a.cos ax.1
(sin ax)′=0+a.cos ax
(sin ax)′=a.cos ax
2. Yol
f′ (x)=h→0limhf (x+h)−f (x)
(sin ax)′=h→0limhsin a(x+h)−sin ax
(sin ax)′=h→0limhsin (ax+ah)−sin ax
sin p−sin q=2.sin (2p−q).cos (2p+q)
(sin ax)′=h→0limh2.sin 2ax+ah−ax.cos 2ax+ah+ax
(sin ax)′=h→0limh2.sin 2ah.cos 22ax+ah
(sin ax)′=h→0limh2.sin 2ah.cos 22.(ax+2ah)
(sin ax)′=h→0limh2.sin 2ah.cos (ax+2ah)
(sin ax)′=h→0lim21.hsin 2ah.cos (ax+2ah)
(sin ax)′=h→0lim2hsin 2ah.cos (ax+2ah)
(sin ax)′=h→0lima.2ha.sin 2ah.cos (ax+2ah)
(sin ax)′=a.h→0lim2ahsin 2ah.cos (ax+2ah)
(sin ax)′=a.h→0lim[2ahsin 2ah.cos (ax+2ah)]
(sin ax)′=a.h→0lim2ahsin 2ah.h→0limcos (ax+2ah)
h→0 (2ah=h)
(sin ax)′=a.h→0limhsin h.h→0limcos (ax+h)
(sin ax)′=a.1.cos (ax+0)
(sin ax)′=a.1.cos ax
(sin ax)′=a.cos ax
3. Yol
sin ax=ax−3!(ax)3+5!(ax)5−7!(ax)7+9!(ax)9−...
cos ax=1−2!(ax)2+4!(ax)4−6!(ax)6+8!(ax)8−...
sin ax=ax−3!(ax)3+5!(ax)5−7!(ax)7+9!(ax)9−...
(sin ax)′=[ax−3!(ax)3+5!(ax)5−7!(ax)7+9!(ax)9−...]′
(sin ax)′=(ax)′−[3!(ax)3]′+[5!(ax)5]′−[7!(ax)7]′+[9!(ax)9]′−...
(sin ax)′=a−3!3.(ax)2.(ax)′+5!5.(ax)4.(ax)′−7!7.(ax)6.(ax)′+9!9.(ax)8.(ax)′−...
(sin ax)′=a−3!3.(ax)2.a+5!5.(ax)4.a−7!7.(ax)6.a+9!9.(ax)8.a−...
(sin ax)′=a−3.2!3.(ax)2.a+5.4!5.(ax)4.a−7.6!7.(ax)6.a+9.8!9.(ax)8.a−...
(sin ax)′=a−2!(ax)2.a+4!(ax)4.a−6!(ax)6.a+8!(ax)8.a−...
(sin ax)′=a.[1−2!(ax)2+4!(ax)4−6!(ax)6+8!(ax)8−...]
(sin ax)′=a.cos ax
Published Date:
July 15, 2024
Updated Date:
April 16, 2025