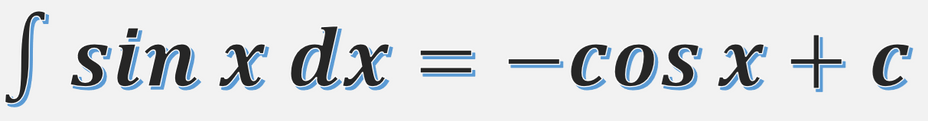
Sin x'in İntegrali (Sinüsün İntegrali)

Sin x'in İntegrali Nedir ?

Sin x'in integrali -cos x'tir.

$\int sinxdx=-cosx+c$

Sin x'in İntegralini Bulma

1. Yol

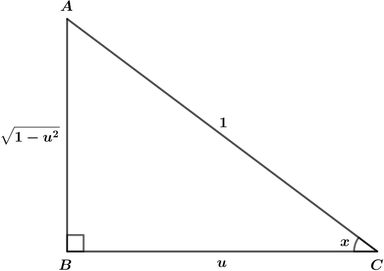
Yukarıdaki ABC dik üçgeninde;

$sinx=\frac{\sqrt{1-u^2}}{1}=\sqrt{1-u^2}$

$cosx=\frac{u}{1}=u$

$\int sinxdx=?$

$sinx=\sqrt{1-u^2}$

$d(sinx)=d(\sqrt{1-u^2})$

$(sinx{)}^{\prime }dx=(\sqrt{1-u^2}{)}^{\prime }du$

$\boxed{(sinx{)}^{\prime }=cosx}$

$\boxed{f(x)=\sqrt{u(x)}\Rightarrow f^{\prime }(x)=\frac{u^{\prime }(x)}{2\sqrt{u(x)}}}$

$cosxdx=\frac{(1-u^2{)}^{\prime }}{2\sqrt{1-u^2}}du$

$udx=\frac{-2udu}{2\sqrt{1-u^2}}$

$dx=\frac{-\cancel{2u}du}{\cancel{2u}\sqrt{1-u^2}}$

$\int sinxdx=\int \cancel{\sqrt{1-u^2}}.\frac{-du}{\cancel{\sqrt{1-u^2}}}$

$\int sinxdx=-\int du$

$\int sinxdx=-u+c$

$\int sinxdx=-cosx+c$

2. Yol

$\int sinxdx=?$

$\boxed{sin2x=2.sinx.cosx}$

$\int sinxdx=\int 2.sin\frac{x}{2}.cos\frac{x}{2}dx$

$sin\frac{x}{2}=u$

$d(sin\frac{x}{2})=du$

$(sin\frac{x}{2}{)}^{\prime }dx=du$

$\boxed{(sinax{)}^{\prime }=a.cosax}$

$\frac{1}{2}cos\frac{x}{2}dx=du$

$cos\frac{x}{2}dx=2du$

$\int sinxdx=\int 2.u.2du$

$\int sinxdx=\int 4udu$

$\int sinxdx=\frac{4u^2}{2}+c$

$\int sinxdx=2u^2+c$

$\int sinxdx=2si{n}^2\frac{x}{2}+c$

$\boxed{1-2si{n}^{2}x=cos2x}$

$1-2si{n}^2\frac{x}{2}=cosx$

$-(1-2si{n}^2\frac{x}{2})=-cosx$

$2si{n}^2\frac{x}{2}-1=-cosx$

$c\in R,c=-1\Rightarrow \int sinxdx=2si{n}^2\frac{x}{2}-1$

$\int sinxdx=-cosx$

3. Yol

$\boxed{sinx=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-...}$

$\boxed{cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-...}$

$\int sinxdx=\int (x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-...)dx$

$\int sinxdx=(\frac{x^2}{2}-\frac{x^4}{4.3!}+\frac{x^6}{6.5!}-\frac{x^8}{8.7!}+\frac{x^{10}}{10.9!}-...)+c$

$\int sinxdx=(\frac{x^2}{2!}-\frac{x^4}{4!}+\frac{x^6}{6!}-\frac{x^8}{8!}+\frac{x^{10}}{10!}-...)+c$

$c\in R,c=-1\Rightarrow \int sinxdx=(\frac{x^2}{2!}-\frac{x^4}{4!}+\frac{x^6}{6!}-\frac{x^8}{8!}+\frac{x^{10}}{10!}-...)-1$

$\int sinxdx=-1+\frac{x^2}{2!}-\frac{x^4}{4!}+\frac{x^6}{6!}-\frac{x^8}{8!}+\frac{x^{10}}{10!}-...$

$\int sinxdx=-(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-\frac{x^{10}}{10!}+...)$

$\int sinxdx=-cosx$