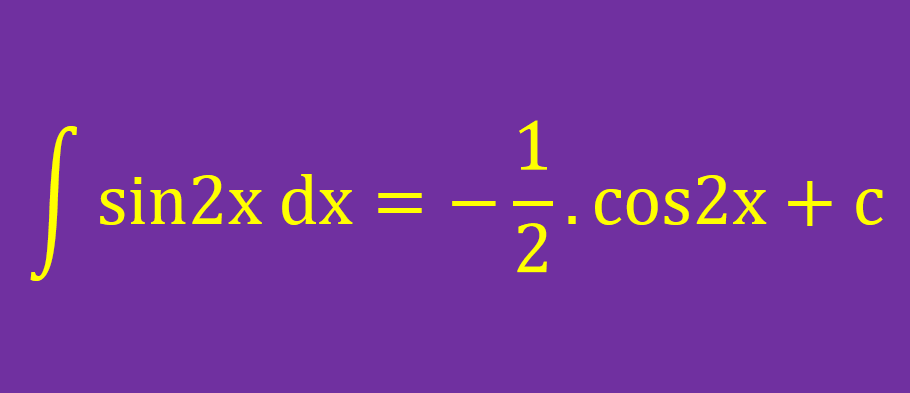Sin2x İntegrali
Sin2x İntegrali Nedir? sin2x'in İntegrali -1/2.cos2x+c'ye eşittir. İspat 1 ∫ sin2x dx = ? 2x = u d(2x) =du (Eşitliği her iki tarafının da diferansiyeli

Pow
@powSin2x İntegrali Nedir?
sin2x'in İntegrali -1/2.cos2x+c'ye eşittir.
İspat 1
∫ sin2x dx = ?
2x = u
d(2x) =du (Eşitliği her iki tarafının da diferansiyelini alırız)
Diferansiyel Alma İşlemi
y = f(x)
dy = df(x)
dy = f(x)'dx
dy/dx = f(x)'
dy/dx = y' = f(x)' olur.
d(2x) =du
(2x)'dx = du
2dx = du
dx = du/2 olur.
2x = u ve dx = du/2
∫ sin2x dx = ∫ sinu du/2
∫ sin2x dx = 1/2.∫ sinu du
∫ sinx dx = -cosx+c olduğunu biliyoruz.
∫ sin2x dx = 1/2.∫ sinu du
∫ sin2x dx = -1/2.cosu+c
∫ sin2x dx = -1/2.cos2x+c olur.
İspat 2
∫ sin2x dx = ?
sin2x = 2.sinx.cosx
∫ sin2x dx = ∫ 2.sinx.cosx dx
sinx = u
d(sinx) = du
(sinx)'dx = du
cosxdx = du
sinx = u ve cosx dx = du
∫ sin2x dx = ∫ 2.u.du
∫ sin2x dx = 2.u²/2 + c
∫ sin2x dx = u² + c
∫ sin2x dx = sin²x + c olur.
Published Date:
January 31, 2021
Updated Date:
December 12, 2023