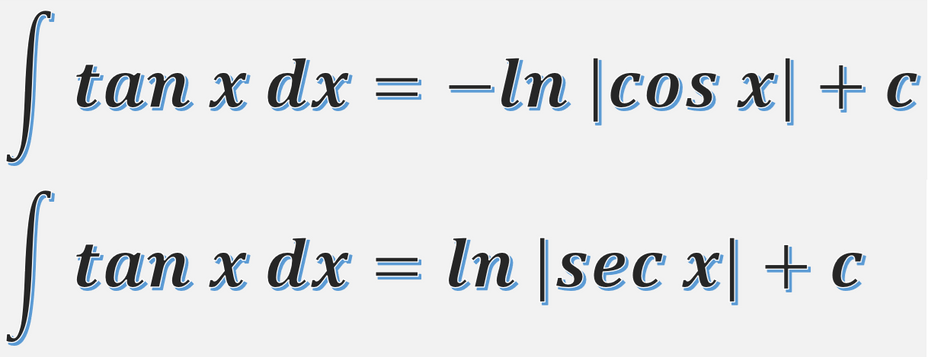
Tan x'in İntegrali (Tanjantın İntegrali)

Tan x'in İntegrali Nedir ?

Tan x'in integrali -ln |cos x|'tir.

$\int tanxdx=-ln|cosx|+c=ln|secx|+c$

Tan x'in İntegralini Bulma

1. Yol

$\int tanxdx=?$

$\boxed{tanx=\frac{sinx}{cosx}}$

$\int tanxdx=\int \frac{sinx}{cosx}dx$

$cosx=u$

$d(cosx)=du$

$(cosx{)}^{\prime }dx=du$

$\boxed{(cosx{)}^{\prime }=-sinx}$

$-sinxdx=du$

$sinxdx=-du$

$\int tanxdx=\int \frac{-du}{u}$

$\int tanxdx=-\int \frac{du}{u}$

$\boxed{\int \frac{dx}{x}=ln|x|+c}$

$\int tanxdx=-ln|u|+c$

$\int tanxdx=-ln|cosx|+c$

$\int tanxdx=ln|co{s}^{-1}x|+c$

$\int tanxdx=ln|\frac{1}{cosx}|+c$

$\boxed{\frac{1}{cosx}=secx}$

$\int tanxdx=ln|secx|+c$

2. Yol

$\int tanxdx=\int \frac{secx}{secx}.tanxdx$

$\int tanxdx=\int \frac{secx.tanxdx}{secx}$

$secx=u$

$d(secx)=du$

$(secx{)}^{\prime }dx=du$

$\boxed{(secx{)}^{\prime }=secx.tanx}$

$secx.tanxdx=du$

$\int tanxdx=\int \frac{du}{u}$

$\int tanxdx=ln|u|+c$

$\int tanxdx=ln|secx|+c$

3. Yol

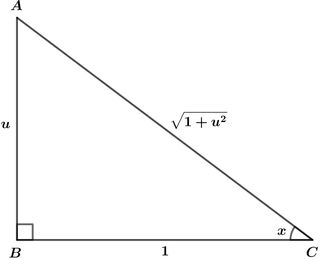
Yukarıdaki ABC dik üçgeninde;

$tanx=\frac{u}{1}=u$

$\int tanxdx=?$

$tanx=u$

$d(tanx)=du$

$(tanx{)}^{\prime }dx=du$

$\boxed{(tanx{)}^{\prime }=1+ta{n}^{2}x}$

$(1+ta{n}^{2}x)dx=du$

$(1+u^2)dx=du$

$dx=\frac{du}{1+u^2}$

$\int tanxdx=\int u.\frac{du}{1+u^2}$

$\int tanxdx=\int \frac{udu}{1+u^2}$

$\int tanxdx=\int \frac{2.udu}{2.(1+u^2)}$

$\int tanxdx=\frac{1}{2}\int \frac{2udu}{1+u^2}$

$1+u^2=v$

$d(1+u^2)=dv$

$(1+u^2{)}^{\prime }du=dv$

$2udu=dv$

$\int tanxdx=\frac{1}{2}\int \frac{dv}{v}$

$\int tanxdx=\frac{1}{2}ln|v|+c$

$\int tanxdx=ln|v^{\frac{1}{2}}|+c$

$\int tanxdx=ln|\sqrt{v}|+c$

$\int tanxdx=ln|\sqrt{1+u^2}|+c$

Yukarıdaki ABC dik üçgeninde;

$secx=\frac{\sqrt{1+u^2}}{1}=\sqrt{1+u^2}$

$\int tanxdx=ln|secx|+c$