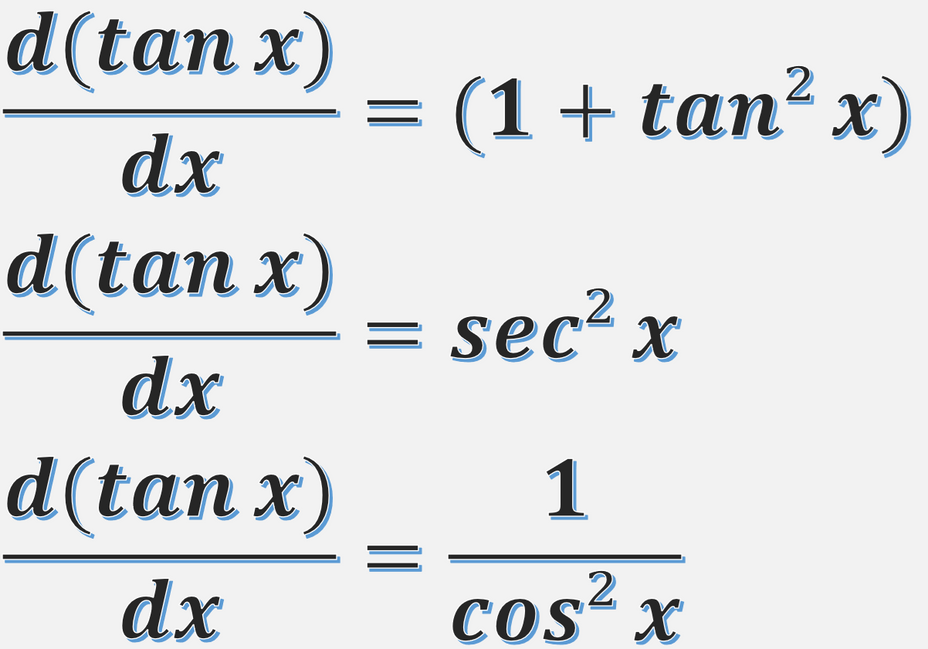Tan x'in Türevi Nedir ?
Tan x'in türevi 1+tan² x'dir.
(tan x)′=1+tan2 x=sec2 x=cos2 x1
dxd(tan x)=1+tan2 x=sec2 x=cos2 x1
Tan x'in Türevinin İspatı
1. Yol
f′ (x)=h→0limhf (x+h)−f (x)
(tan x)′=h→0limhtan (x+h)−tan x
tan (p+q)=1−tan p.tan qtan p+tan q
(tan x)′=h→0limh1−tan x.tan htan x+tan h−tan x
(tan x)′=h→0limh1−tan x.tan htan x+tan h−tan x.(1−tan x.tan h)
(tan x)′=h→0limh1−tan x.tan htan x+tan h−tan x+tan2 x.tan h
(tan x)′=h→0limh1−tan x.tan htan h+tan2 x.tan h
(tan x)′=h→0limh1−tan x.tan htan h.(1+tan2 x)
(tan x)′=h→0lim [h1.1−tan x.tan htan h.(1+tan2 x)]
(tan x)′=h→0limh.(1−tan x.tan h)tan h.(1+tan2 x)
(tan x)′=h→0lim (htan h.1−tan x.tan h1+tan2 x)
(tan x)′=h→0limhtan h.h→0lim1−tan x.tan h1+tan2 x
t→0limttan t=1
(tan x)′=1.1−tan x.tan 01+tan2 x
(tan x)′=1−tan x.tan 01+tan2 x
tan 0=0
(tan x)′=1−tan x.01+tan2 x
(tan x)′=1−01+tan2 x
(tan x)′=11+tan2 x
(tan x)′=1+tan2 x
2. Yol
f′ (x)=h→0limhf (x+h)−f (x)
(tan x)′=h→0limhtan (x+h)−tan x
tan x=cos xsin x
(tan x)′=h→0limhcos (x+h)sin (x+h)−cos xsin x
(tan x)′=h→0limhcos x.cos (x+h)sin (x+h).cos x−cos (x+h).sin x
sin p.cos q−cos p.sin q=sin (p−q)
(tan x)′=h→0limhcos x.cos (x+h)sin (x+h−x)
(tan x)′=h→0limhcos x.cos (x+h)sin h
(tan x)′=h→0lim [h1.cos x.cos (x+h)sin h]
(tan x)′=h→0limh.cos x.cos (x+h)sin h
(tan x)′=h→0lim [hsin h.cos x.cos (x+h)1]
(tan x)′=h→0limhsin h.h→0limcos x.cos (x+h)1
t→0limtsin t=1
(tan x)′=1.cos x.cos (x+0)1
(tan x)′=cos x.cos (x+0)1
(tan x)′=cos x.cos x1
(tan x)′=cos2 x1
3. Yol
tan x=cos xsin x
(tan x)′=(cos xsin x)′
(vu)′=v2u′.v−v′.u
(tan x)′=cos2 x(sin x)′.cos x−(cos x)′.sin x
(sin x)′=cos x (cos x)′=−sin x
(tan x)′=cos2 xcos x.cos x−(−sin x).sin x
(tan x)′=cos2 xcos2 x+sin2 x
cos2 x+sin2 x=1
(tan x)′=cos2 x1
(tan x)′=(cos x1)2
cos x1=sec x
(tan x)′=sec2 x
Soru
y=tan (3−4x)⇒y′= ?
1. Cevap
y=tan (3−4x)
dy=d[tan (3−4x)]
dy=[tan (3−4x)]′ dx
dxdy=[tan (3−4x)]′
u=3−4x
du=d(3−4x)
du=(3−4x)′ dx
du=−4 dx
dxdu=−4
y=tan u
dy=d(tan u)
dy=(tan u)′ du
dy=(1+tan2 u) du
dudy=1+tan2 u
dxdu.dudy=dxdy
−4.(1+tan2 u)=[tan (3−4x)]′
−4.[1+tan2 (3−4x)]=[tan (3−4x)]′
2. Cevap
(tan u)′=u′.(1+tan2 u)
[tan (3−4x)]′=(3−4x)′.[1+tan2 (3−4x)]
[tan (3−4x)]′=−4.[1+tan2 (3−4x)]
Published Date:
June 27, 2020
Updated Date:
February 05, 2025