15 75 90 Üçgeni

İç açılarının ölçüleri 15°, 75° ve 90° olan üçgene 15 75 90 üçgeni denir. Yukarıdaki şekildeki ABC üçgeni bir 15 75 90 üçgenidir.

15 75 90 Üçgeni Kenarları

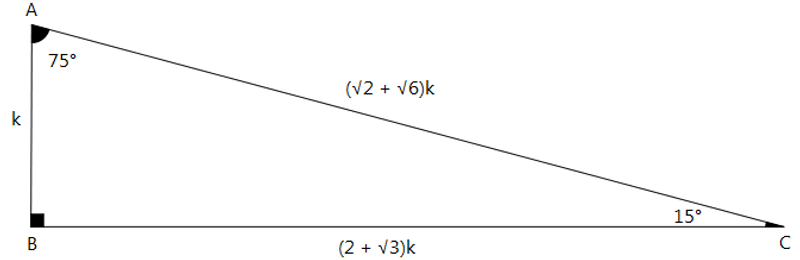
Bir 15 75 90 üçgeninde, 15°'lik açının karşısındaki kenarın uzunluğuna k dersek 75°'lik açının karşısındaki kenarın uzunluğu (2 + √3)k ve 90°'lik açının karşısındaki kenarın (hipotenüsün) uzunluğu da (√2 + √6)k olur.

15 75 90 Üçgeni İspatı

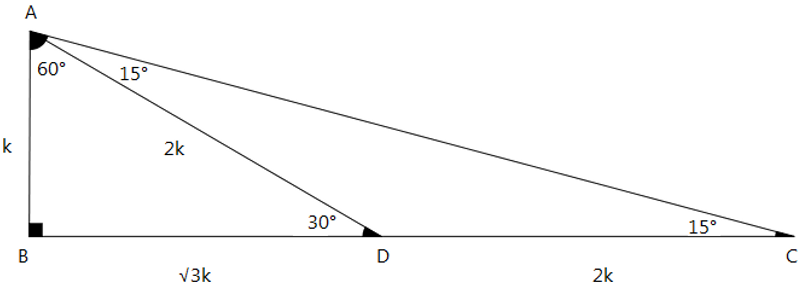
Yukarıdaki şekildeki ABD üçgeni bir 30 60 90 üçgenidir. 30 60 90 üçgeninde 90°'lik açının karşısındaki kenarın (hipotenüsün) uzunluğu 30°'lik açının karşısındaki kenarın uzunluğunun 2 katı ve 60°'lik açının karşısındaki kenarın uzunluğu da 30°'lik açının karşısındaki kenarın uzunluğunun √3 katıdır.

AB kenarının uzunluğuna k dersek AC kenarının uzunluğu 2k ve BD kenarının uzunluğu da √3k olur. CAD açısının ölçüsü ile DCA açısının ölçüsü birbirine eşit olduğu için, AD kenarı ile DC kenarının uzunluğu birbirine eşit olur.

|AB| = k

|BD| = √3k

|AD| = |DC| = 2k

Yukarıdaki şekildeki ABC üçgenine Pisagor Teoremi'ni uygularsak;

|AC|² = |AB|² + |BC|² olur.

|AC|² = |AB|² + |BC|²

|AC|² = k² + ((2 + √3)k)²

|AC|² = k² + (2 + √3)²k²

|AC|² = k² + (2² + 2.2.√3 + √3²)k²

|AC|² = k² + (4 + 4√3 + 3)k²

|AC|² = k² + (7 + 4√3)k²

|AC|² = (1+7 + 4√3)k²

|AC|² = (8 + 4√3)k²

|AC|² = (8 + 2.2√3)k²

|AC|² = (8 + 2√2².3)k²

|AC|² = (8 + 2√4.3)k²

|AC|² = (8 + 2√12)k²

|AC|² = (2 + 6 + 2√2.6)k²

|AC|² = (√2² + √6² + 2√2.√6)k²

|AC|² = (√2 + √6)²k²

|AC| = (√2 + √6)k olur.

15 75 90 üçgeninde 90°'lik açının karşısındaki kenarın (hipotenüsün) uzunluğu (√2 + √6)k'dir.

15 75 90 Üçgeni Özellikleri

1. 15 75 90 Üçgeninin kenar uzunluklarının toplamı (√2 + √3 + √6 + √9).k'dir.

2. 15 75 90 Üçgeninin alanı (1 + √3/2)k²/2'dir.

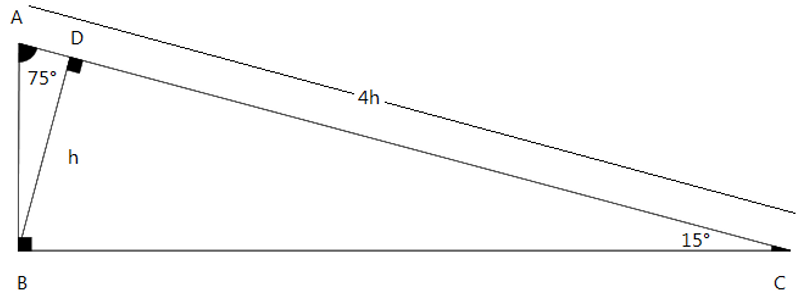
3. 15 75 90 Üçgeninde hipotenüse ait yüksekliğin uzunluğu hipotenüsün uzunluğunun 1/4'ü kadardır. h = (√2 + √6)k/4

Yukarıdaki şekilde |AC| = 4.|BD|'dir.

İspat

|AC|.|BD|/2 = |AB|.|BC|/2

|AC|.|BD| = |AB|.|BC|

(√2 + √6)k.h = k.(2 + √3)k

(√2 + √6).h = (2 + √3)k

h = (2 + √3)k/(√2 + √6)

h = (2 + √3)(√2 - √6)k/(√2 + √6)(2 - √6)

h = (2√2 - 2√6 + √3.√2 - √3.√6)k/(√2² - √6²)

h = (2√2 - 2√6 + √6 - √18)k/(2 - 6)

h = (2√2 - 2√6 + √6 - 3√2)k/-4

h = (-√2 - √6)k/-4

h = (√2 + √6)k/4 olur.