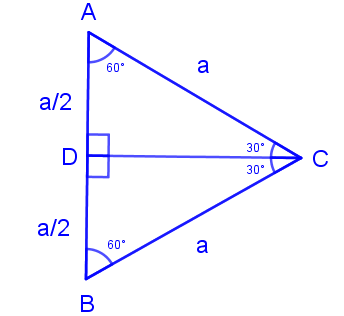
Yukarıdaki şekildeki ABC üçgeni bir eşkenar üçgendir. [CD] Doğru parçası aynı anda hem açıortay, hem kenarortay, hem yükseklik hem de bir orta dikme olup, uzunlukları birbirine eşittir.
Açıortay C açısını tam ortasından 30°'lik iki eşit parçaya bölerken, kenarortay da AB doğru parçasını tam ortasından iki eşit parçaya ayırır.
30 60 90 üçgeni kuralı
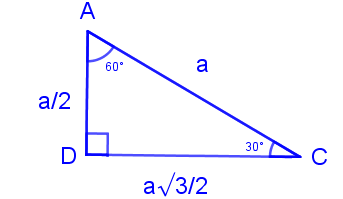
Yukarıdaki eş kenar üçgeni iki eşit parçaya ayırdığımızda elde ettiğimiz üçgene "30-60-90 Üçgeni" denir.
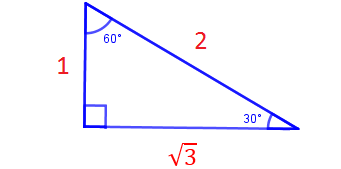
30-60-90 Üçgeninde 30°'nin karşısındaki kenarın uzunluğu, en büyük (90°'nin karşısındaki kenar) kenar olan hipotenüsün uzunluğunun 1/2'si kadardır. 60°'nin karşısındaki kenarın uzunluğu ise hipotenüsün uzunluğunun √3/2 katı kadardır.
ADC üçgenine Pisagor Teoremini uygularsak;
|AD|² + |DC|² = |AC|²
(a/2)² + |DC|² = a²
a²/4 + |DC|² = a²
|DC|² = a² - a²/4
|DC|² = 3a²/4
√|DC|² = √3a²/4
|DC| = a√3/2 olur.
30 60 90 üçgeni özellikleri
1. Çevresi
a(3 + √3)/2
2. Alanı
a²√3/8
3. Hipotenüse ait Yükseklik
a²√3/4
30 60 90 üçgeni trigonometrik oranları
30° için
sin30° = 1/2
cos30° = √3/2
tan30° = 1/√3
cot30° = √3
60° için
sin60° = √3/2
cos60° = 1/2
tan60° = √3
cot60° = 1/√3
