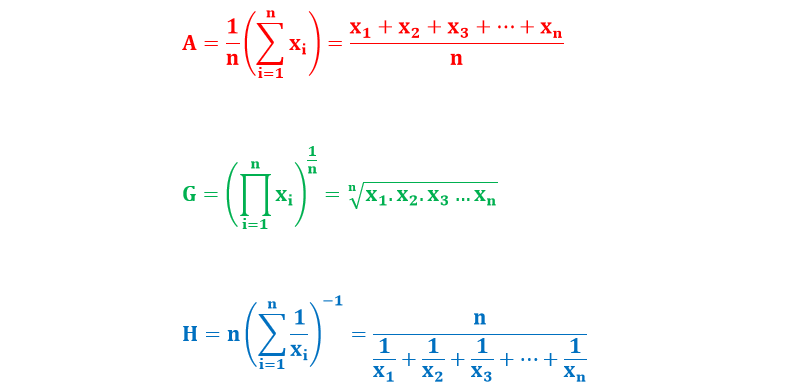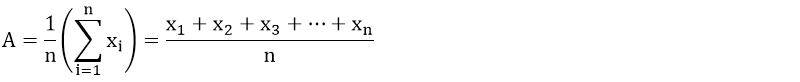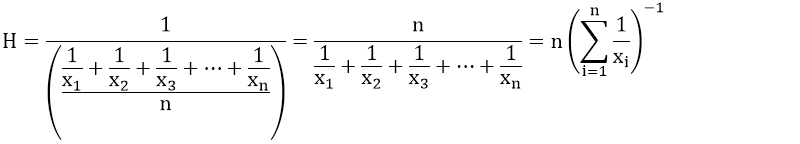Aritmetik Ortalama Geometrik Ortalama Harmonik Ortalama

1. Aritmetik Ortalama Nedir?

Eski Yunanca kökenli bir sözcük olan "aritmetik" dilimize Fransızca'dan geçmiştir. Eski Yunanca'da, "sayı" anlamına gelen "aritmos" sözcüğünden türemiş olan "aritmetiki", "sayı saymaya ilişkin" anlamına gelmektedir.

Bir gözleme veya ölçüme dayalı olarak elde edilmiş olan verilerin toplamının toplam veri sayısına bölünmesiyle elde edilen değere (büyüklüğe) aritmetik ortalama veya kısaca ortalama denir.

Aritmetik Ortalama Nasıl Hesaplanır? (Aritmetik Ortalamanın Formülü)

Aritmetik Ortalamanın Özellikleri

1. Aritmetik ortalamadan sapmaların toplamı sıfırdır.

2. Veri değerlerinde meydana gelen değişimler çok küçük de olsa aritmetik ortalama bu değişimlerden etkilenir.

3. Aritmetik ortalama tüm verilerin hesaplamada kullanması nedeni ile güçlü bir istatistiki ölçümdür.

4. Uç veri değerlerden etkilenmesi aritmetik ortalamanın zayıf yönünü oluşturur.

Örnek 1

Bir basketbol takımınındaki basketbolcuların yaşları küçükten büyüğe doğru sırasıyla; 18, 23, 25, 29 ve 32'dir. Bu basketbol takımının yaş ortalaması kaçtır?

Çözüm 1

Takımın Yaş Ortalaması = (18 + 23 + 25 + 29 + 32) / 5 = 127 / 5 = 25,40

Örnek 2

Bir iş yerinde çalışmakta olan bayan işçilerin yaşlarının ortalaması 27 ve erkek işçilerin yaşlarının ortalaması ise 36'dır. Bu iş yerinde 10 bayan ve 15 erkek işçi çalıştığına göre iş yerindeki tüm çalışanların (bayan ve erkek) yaşlarının ortalaması kaç olur?

Çözüm 2

Bayan İşçilerin Yaşları Toplamı / Bayan İşçi Sayısı = Bayan İşçilerin Yaşlarının Ortalaması

Bayan İşçilerin Yaşları Toplamı / 10 = 27

Bayan İşçilerin Yaşları Toplamı = 27 x 10 = 270

Erkek İşçilerin Yaşları Toplamı / Erkek İşçi Sayısı = Erkek İşçilerin Yaşlarının Ortalaması

Erkek İşçilerin Yaşları Toplamı / 15 = 36

Erkek İşçilerin Yaşları Toplamı = 36 x 15 = 540

Tüm Çalışanların Yaşlarının Ortalaması = Tüm Çalışanların Yaşları Toplamı / Tüm Çalışanların Sayısı

Tüm Çalışanların Yaşlarının Ortalaması = 270 + 540 / 10 + 15

Tüm Çalışanların Yaşlarının Ortalaması = 810 / 25 = 32.40'dır.

2. Geometrik Ortalama Nedir?

Bir gözleme veya ölçüme dayalı olarak elde edilmiş olan verilerin birbirleriyle çarpımlarının n veri sayısı olmak üzere n. dereceden kökü ile ifade edilen değere (büyüklüğe) geometrik ortalama denir.

Geometrik Ortalama Nasıl Hesaplanır? (Geometrik Ortalamanın Formülü)

Geometrik Ortalamanın Özellikleri

1. Bir gözleme veya ölçüme dayalı olarak elde edilmiş olan verilerin geometrik ortalaması aritmetik ortalamasından her zaman için küçük veya eşittir.

2. Geometrik ortalamayı bulmak için kullanılacak olan veri değerlerinin daima pozitif olması gerekir. Eğer tek bir veri değeri dahi sıfır olur ise geometrik ortalama anlamsız olur.

3. Geometrik ortalama, uç veri değerlerden aritmetik ortalama kadar etkilenmez.

4. Gözlem veya ölçüm sonuçlarının her biri bir önceki gözlem veya ölçüm sonucuna bağlı olarak değişiyor ve bu değişmenin hızı saptanmak isteniyorsa geometrik ortalamayı kullanmak daha anlamlıdır.

5. Her bir öğenin farklı sayısal aralıklara sahip birden fazla özelliğe sahip olduğu durumlarda, farklı öğeleri karşılaştırırken bu öğeler için tek bir değer bulmak için Geometrik ortalama kullanılabilir.

Örnek 1

4, 8, 16 ve 32 şeklindeki terimlerden oluşan bir dizinin geometrik ortalamasını bulunuz?

Çözüm 1

Yukarıdaki dizinin terimleri geometrik şekilde artış gösterdiğinden dolayı dizinin aritmetik ortalamasını hesaplamak pek anlamlı olmaz. Dizinin geometrik ortalamasını hesaplamak daha anlamlı olur.

G = ∜4.8.16.32

G = ∜16384

G = 11, 3137 olur.

Örnek 2

A üniversitesinden mezun olmuş olan bir öğrencinin 4'lük sisteme göre mezuniyet ortalaması 3,62 ve 100'lük sisteme göre mezuniyet ortalaması ise 87,29'dur. B üniversitesinden mezun olmuş olan bir başka öğrencinin ise 4'lük sisteme göre mezuniyet ortalaması 3,54 ve 100'lük sisteme göre mezuniyet ortalaması ise 88,63'dür. Bu öğrencilerden hangisi daha başarılıdır?

Çözüm 2

Burada aritmetik ortalamayı kullanmak değerlendirme iki farklı ölçeğe göre yapıldığı için pek uygun ve sağlıklı olmaz. Geometrik ortalamayı kullanmak daha doğru ve sağlıklı sonuç verir.

G (A) = √3,62x87,29 = √315,9898 = 17,7761

G (B) = √3,54x88,63 = √313,7502 = 17,7130

G (A) > G (B) olduğu için A üniversitesinden mezun olan öğrenci B üniversitesinden mezun olan öğrenciden daha başarılıdır.

3. Harmonik Ortalama Nedir?

Bir gözleme veya ölçüme dayalı olarak elde edilmiş olan verilerin çarpma işlemine göre terslerinin ortalamasının tersinin alınmasıyla elde edilen değere (büyüklüğe) harmonik ortalama denir. Hamonik ortalama özellikle basit veriler için oldukça kullanışlıdır.

Harmonik Ortalama Nasıl Hesaplanır? (Harmonik Ortalamanın Formülü)

Harmonik Ortalamanın Özellikleri

1. Genellikle, ekonomi ile ilgili verilerin hesaplanması sırasında 1 birim ile alınan ortalama miktara veya bir mamülün bir biriminin üretimi için harcanan ortalamaya gereksinim duyulduğunda kullanılır.

2. Fizikte; ortalama hız, bir karışımın yoğunluğu ve paralel bağlı dirençlerin hesaplanmasında kullanınılır.

3. Harmonik ortalama geometrik ve aritmatik ortalamadan her zaman için küçük veya eşittir.

Örnek 1

Bir araç A ve B şehirleri arasındaki mesafenin 1/3'ünü 40 km/s hızla ve 2/3'ünü ise 100 km/s hızla katetmiştir. Aracın yol boyuncaki ortalama hızı ne olur?

Çözüm 1

1/H = (1.1/40 + 2.1/100)/3

1/H = (1/40 + 2/100)/3

1/H = (1/40 + 1/50)/3

1/H = [(40 + 50)/40.50]/3

1/H = (90/2000)/3

1/H = (9/200)/3

1/H = 9/200.1/3

1/H = 9.1/200.3

1/H = 3/200

H = 200/3

H = 66,66 km/s olur.