Asal Sayılar

Asal Sayı Nedir?

1 ve kendisinden başka ortak böleni olmayan 1’den büyük pozitif tam sayılara asal sayı denir. Örneğin, eğer n sayısı (n>2) bir asal sayı ise yalnız ve yalnız 1 ve n sayısına bölünebilir. 2, 3, 4, … n-1 sayılarından hiçbirisi n sayısını bölemez.

1, bir asal sayı değildir çünkü 1’den başka ortak bir böleni yoktur.

2, bir asal sayıdır çünkü 1 ve kendisinden (2’den) başka ortak bir böleni yoktur.

3, bir asal sayıdır çünkü 1 ve kendisinden (3’ten) başka ortak bir böleni yoktur. (2’ye bölünmez)

4, bir asal sayı değildir çünkü 1 ve kendisinden (4’ten) başka 2’ye de bölünür. (2 ve 3 sayılarından en az birine bölünür)

5, bir asal sayıdır çünkü 1 ve kendisinden (5’ten) başka ortak bir böleni yoktur. (2, 3 ve 4’e bölünmez)

6, bir asal sayı değildir çünkü 1 ve kendisinden (6’dan) başka 2'ye ve 3’e de bölünür. (2, 3, 4 ve 5 sayılarından en az birine bölünür)

7, bir asal sayıdır çünkü 1 ve kendisinden (7’den) başka ortak bir böleni yoktur. (2, 3, 4, 5 ve 6’ya bölünmez)

8, bir asal sayı değildir çünkü 1 ve kendisinden (8’den) başka 2'ye ve 4’e de bölünür. (2, 3, 4, 5, 6 ve 7 sayılarından en az birine bölünür)

9, bir asal sayı değildir çünkü 1 ve kendisinden (9’dan) başka 3’e de bölünür. (2, 3, 4, 5, 6, 7, 8 sayılarından en az birine bölünür)

10, bir asal sayı değildir çünkü 1 ve kendisinden (10’dan) başka 2'ye ve 5’e de bölünür. (2, 3, 4, 5, 6, 7, 8 ve 9 sayılarından en az birine bölünür)

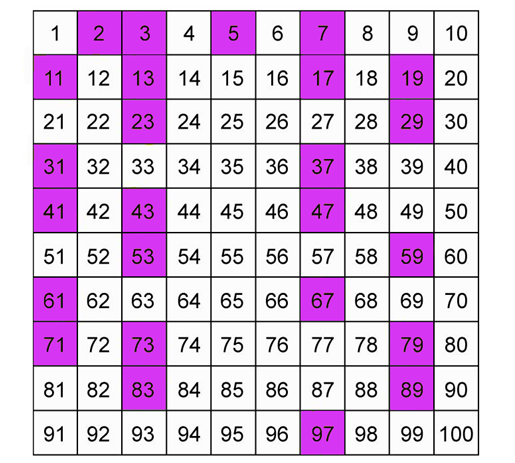
Yukarıda da görüleceği üzere 1’den 10’a kadar olan sayılarından 2, 3, 5 ve 7 asıl sayı iken 1, 4, 6, 8, 9 ve 10 asal sayı değildir.

Asal Sayı Tablosu

1 Neden Asal Sayı Değildir?

1’in asal bir sayı olarak kabul edilmemesinin nedeni tek bir böleninin olmasıdır. Ama bu öyle bir bölendir ki, sonsuz kez yinelenebilir.

Bütün sayılar asal çarpanların bir çarpımı olarak yazılabilir.

4 = 2 x 2

6 = 2 x 3

10 = 2 x 5

24 = 2 x 2 x 2 x 3

30 = 2 x 3 x 5

50 = 2 x 5 x 5

Peki, şimdi de 15 sayısını asal çarpanların bir çarpımı olarak yazılım.

15 = 3 x 5

15 = 3 x 5 x 1

15 = 3 x 5 x 1 x 1

15 = 3 x 5 x 1 x 1 x 1

Şeklinde de yazılabilir ve istediğimiz kadar 1 koyarak bunu daha da uzatabiliriz. Böylelikle 1 sayısının asal olmadığı buradan da kolaylıkla anlaşılabilir.

Asal sayıları ilginç yapan özelliklerinden biri de herhangi bir kurala uymamaları ve bir matematik formülü ile (en azından bugüne kadar) ifade edilememeleridir. Çünkü asal sayılar karşımıza herhangi bir sırayla veya düzen de değil de rastgele olarak çıkarlar.

Örneğin;

0 ile 10 arasında; 2, 3, 5 ve 7 olmak üzere 4 tane asal sayı bulunur.

10 ile 20 arasında; 11, 13, 17 ve 19 olmak üzere 4 tane asal sayı bulunur.

20 ile 30 arasında; 23 ve 29 olmak üzere 2 tane asal sayı bulunur.

30 ile 40 arasında; 31 ve 37 olmak üzere 2 tane asal sayı bulunur.

40 ile 50 arasında; 41, 43 ve 47 olmak üzere 3 tane asal sayı bulunur.

Yukarıdan da anlaşılacağı üzere 0 ile 50 arasında 15 tane asal sayı bulunmaktadır. Ancak bu hep böyle gitmez mesela 50 ile 100 arasında (53, 59, 61, 67, 71, 73, 79, 83, 89 ve 97) olmak üzere yalnızca 10 tane asal sayı vardır.

Neden Sonsuz Tane Asal Sayı Vardır?

Bundan yaklaşık 2300 yıl önce yaşamış olan İskenderiyeli ünlü matematikçi Öklid’in de kanıtlamış olduğu gibi sonsuz tane asal sayı vardır.

Öklit sonsuz tane asal sayı olduğunu olmayana ergi metoduna göre ispatlamıştı. Bu yönteme göre, ispatlanmak istenilen yargının tersi söylenerek onun yanlış olduğu ispatlanır. Şimdi ispatımıza geçelim.

1’den büyük herhangi bir sayıyı asal çarpanlarına ayırarak yazabiliriz.

Örneğin, 5 (5), 6 (2 x 3), 11 (11), 18 (2 x 3 x 3), 40 (2 x 2 x 2 x 5), 83 (83) gibi

Asal sayıların sonlu olduğunu ve en büyük asal sayımızın da A olduğunu kabul edelim.

Bütün asal çarpanları bulunduran ve asal olmayan en büyük sayımız S olsun.

2 = 2

6 = 2 x 3

30 = 2 x 3 x 5

210 = 2 x 3 x 5 x 7

… = …

S = 2 x 3 x 5 x 7 x 11 x 13 x … x A

S + 1 = 2 x 3 x 5 x 7 x 11 x 13 x … x A + 1 olur.

S sayımız bir asal sayı olamayacağına göre (asal çarpanlarına ayrıldığı için) S + 1 sayımızın da bir asal sayı olmaması için bütün asal çarpanlara (2, 3, 5, 7, …, A) bölünmesi gerekmektedir. Ancak yukarıdaki eşitliğin sağ tarafındaki sayıyı 2’den başlamak üzere sırasıyla 3, 5, 7, …, A asal çarpanlarına böldüğümüzde hep 1 kalanını elde ederiz. Bir sayının 1 kalanını vermesi demek onun asal çarpanlarına ayrılamaması anlamına gelebilir. Asal çarpanlarına ayrılamayan bir sayının kendisi de zaten bir asal sayıdır. O zaman S + 1 bir asal sayı olduğuna ve A asal sayısından da daha büyük bir değere sahip olacağına göre her asal sayıdan daha büyük bir asal sayı mutlaka bulunmaktadır. O zaman asal sayılar sonsuz tanedir.

Örneğin, asal sayılar kümesinin sadece 2, 3, 5 ve 7 sayılarından oluştuğunu ve en büyük asal sayımızın da 7 olduğunu kabul edelim. Bu asal sayıların tümünü bir kere kullanarak elde edeceğimiz sayıyı aşağıya yazalım.

S = 2 x 3 x 5 x 7

S = 210

S + 1 = 210 + 1

S + 1 = 211

211 sayısını 2, 3, 5 ve 7 sayılarına sırasıyla böldüğümüzde hep 1 kalanını elde ederiz. 1 kalanını veren bir sayı asal bir sayı olabilir (3, 5, 7, 11 ve 13 gibi) gerçekten 311 sayısının 1 ve 311’den başka ortak bir böleni yoktur. O zaman 311 sayısı asal bir sayıdır ve bizim 7’den büyük bir asal sayı yoktur varsayımımız doğru çıkmamıştır.

S + 1 bir asal sayı değil ise eğer bu S + 1’in A’dan büyük birtakım asal sayıların çarpımı şeklinde yazılabileceği anlamına gelmektedir. O zaman bu durum her daim A’dan büyük bir asal sayının olacağı anlamına gelmektedir. O zaman asal sayılar sonsuza kadar gider demektir.

Örneğin, asal sayılar kümesinin sadece 2, 3, 5, 7, 11 ve 13 sayılarından oluştuğunu ve en büyük asal sayımızın da 13 olduğunu kabul edelim. Bu asal sayıların tümünü bir kere kullanarak elde edeceğimiz sayıyı aşağıya yazalım.

S = 2 x 3 x 5 x 7 x 11 x 13

S = 30030

S + 1 = 30030 + 1

S + 1 = 30031

30031 sayısı bir asal sayı değildir çünkü 59 x 509 şeklinde iki tane asal çarpanı vardır. 59 ve 509 asal sayıları 13 asal sayısından büyük olduğuna göre 13’ten büyük bir asal sayı yoktur varsayımımız doğru çıkmamıştır. O zaman sonsuz tane asal sayı var demektir.

Asal Sayıca Zengin Formüller

Asal sayılar herhangi bir kurala uymadıklarından dolayı bunları saptamaya yarayacak genel bir formül elde etme girişimleri en azından bugüne kadar herhangi bir sonuç vermemiştir. Ancak bunlardan bazıları başlangıçta umut verici gözükmüştür.

Örneğin, p² + p + 11 formülünde p yerine 0, 1, 2, 3, 4, 5, 6, 7, 8 ve 9 sayılarını koyduğumuzda hep bir asal sayı elde ederiz ancak p yerine 10 yazdığımızda elde ettiğimiz değer bir asal sayı olmayan 121’dir. Çünkü 121, 11 ile 11’in çarpımıdır.

Böyle formüllere çok sayıda asal sayı verdiği için asal sayıca zengin formüller denir.

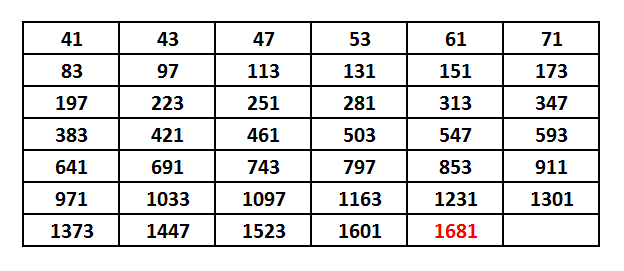
Bu formüllerin en ünlülerinden biride, 18. yüzyılda yaşamış ve matematiğin dehası olarak kabul edilen İsviçreli matematikçi Leonhard Euler’in bulmuş olduğu p² + p + 41 formülüdür. Formülümüz de p yerine 0’dan başlamak üzere 39’a kadar verdiğimiz bütün değerler için elde ettiğimiz sayılar asaldır. Ancak p = 40 için elde ettiğimiz sayı olan 1681 bir asal sayı değildir. Çünkü 1681, 41 ile 41’in çarpımına eşittir.

p² + p + 41 formülünde p = 40 için

40² + 40 + 41

40.40 + 1.40 + 41

40.(40 + 1) + 41

40.41 + 41

40.41 + 1.41

(40 + 1).41

41.41 = 1681

Kendimiz de birçok asal sayı elde edebileceğimiz bir formül bulabiliriz.

Örneğin, 3p + 2 formülünü kullanarak birçok asal sayı elde edebiliriz. p yerine sırasıyla 1, 3, 5, 7, … tek sayılarını koyalım.

5, 11, 17, 23, 29, 35, 41, 47

Yukarıda da görüleceği gibi elde ettiğimiz ilk birkaç sayıdan 35’in dışındakilerin hepsi asal sayıdır.

Aralarında Asal Sayılar

Birden başka ortak böleni olmayan iki pozitif tam sayıya aralarında asal sayılar denir. Aralarında asal olan sayıların mutlaka asal sayı olmaları gerekmez.

(7, 11), (10, 23), (15, 37), (13, 15) aralarında asal sayılara örnek olarak verilebilir.

Asal olmayan iki sayı aralarında asal sayı olabilir (9, 20)

İki çift sayı hiçbir zaman aralarında asal sayı olamaz (8, 14)

İki asal sayı aralarında da asaldır (7, 13)

Sayılardan biri tek veya asal sayı ise iki sayı aralarında asal sayı olmayabilirler (3, 12), (15, 27)

Ardışık sayılar (1, 2, 3, 4, . . . n) kesinlikle aralarında asal sayılardır. (5, 6), (12,13)

Fermat Asalları

Fransız amatör matematikçi Pierre de Fermat’da asal sayılar üzerinde çalışmış ve aşağıdaki formülde n yerine 0’dan başlamak üzere yazacağımız her doğal sayı için elde edeceğimiz sayının asal sayı olacağını iddia etmiştir. Fermat’nın ortaya attığı bu iddianın 17. yüzyıl boyunca doğru olduğu düşünüldü ve n yerine yazılan bütün doğal sayıların asal sayı vereceği kabul edildi. Ancak Euler n = 5 için elde edilen Fermat sayısı olan 4294967279’un asal bir sayı olmadığını 641 ile 6700417 sayılarının çarpımına eşit olduğunu bulunca bunun doğru olmadığı kanıtlanmış oldu. Euler aynı sonucun 6 ve 7 sayıları içinde geçerliği olduğunu kanıtladı ve o günden bu güne geçen süre de henüz n = 4’den büyük başka bir Fermat asalı bulunamamıştır.

Yukarıdaki formül de n yerine sırasıyla 0, 1, 2, 3 ve 4 yazdığımız da elde ettiğimiz sayıların hepsi asal sayıdır.

Mersenne Sayıları ve Mersenne Asalları

Mersenne sayıları, matematikte ikinin üssünün bir eksiği şeklinde tanımlanan sayılardır ve n bir doğal sayı olmak üzere aşağıdaki formüle göre hesaplanırlar.

Mersenne asal sayıları, hem bir Mersenne sayısı, hem de bir asal sayı olan sayılardır.

n = 0 için 2⁰ - 1 = 1 - 1 = 0

n = 1 için 2¹ - 1 = 2 - 1 = 1

n = 2 için 2² - 1 = 4 - 1 = 3

n = 3 için 2³ - 1 = 8 - 1 = 7

n = 4 için 2⁴ - 1 = 16 - 1 = 15

n = 5 için 2⁵ - 1 = 32 - 1 = 31

n = 6 için 2⁶ - 1 = 64 - 1 = 63

n = 7 için 2⁷ - 1 = 128 - 1 = 127 şeklinde sonsuza kadar devam eder gider.

Yukarıdaki Mersennes sayılarından 3, 7, 31 ve 127 Mersennes asallarıdır ve günümüzde bilinen en büyük asal sayıların büyük bir kısmı Mersenne asallarından oluşmaktadır.

Goldbach Hipotezi

Goldbach sanısı olarak ta bilinen ve Alman matematikçi Christian Goldbach’ın ortaya attığı "2'den büyük her çift sayı, iki asal sayının toplamı şeklinde yazılabilir" iddiasıdır. Örneğin;

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 veya 5 + 5

12 = 5 + 7

14 = 3 +11 veya 7 + 7

16 = 3 + 13 veya 5 + 11

18 = 5 + 13 veya 7 + 11

20 = 3 + 17 veya 7 + 13

Goldbach’ın bu hipotezi ilk bakışta doğru gibi gözükse de bütün çift sayıların iki asal sayının toplamı şeklinde yazılıp yazılamayacağı henüz ispatlanamamış ve sayılar teorisinin gizemini koruyan konularından biri olmaya devam etmektedir.

İkiz Asallar

Aralarındaki fark 2 olan asal sayı çiftlerine İkiz asallar denir. Örneğin (3 ile 5), (5 ile 7) ve (11 ile 13) ikiz asallardır. 2 ile 3 çifti hariç iki asal sayı arasındaki fark zaten her zaman en az 2 olmak zorundadır.

İkiz asalların sonsuz tane olup olmadığı ile ilgili soru, sayılar kuramının yıllardır çözülememiş en büyük problemlerinden birisidir ve "ikiz asallar sanısı (varsayımı,kestirimi)" olarak adlandırılır.

İlk 20 ikiz asal sayı çifti;

(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283) ve (311, 313).

En Büyük Asal Sayı

Yukarıda da belirttiğimiz gibi sonsuz sayıda asal sayı vardır. Günümüz de yeni asal sayılar bulmak ve bir önceki elde edilen asal sayıdan daha büyük bir asal sayı elde etmek için yüksek hızlı bilgisayarlardan yararlanılmaktadır. Ancak her defasında bir öncekinden daha büyük bir asal sayı bulmak yine de oldukça zor bir iştir.

Bugün bilinen en büyük asal sayı 2⁸²⁵⁸⁹⁹³³ - 1 sayısıdır ve 24.862.048 basamaktan oluşmaktadır. Bundan önce bilinen en büyük asal sayı ise yine bir Mersenne Sayısı olan 2⁷⁷²³²⁹¹⁷ - 1'di ve 23.249.425 basamaktan oluşmaktaydı.

Asal Sayılar ve Şifreleme

İki çok büyük asal sayının çarpımından oluşan bir sayıyı asal çarpanlarına ayırmak oldukça zor ve zaman alıcı bir iş olduğundan gizli şifrelerin oluşturulmasında asal sayıların belirli bir önemi bulunmaktadır.

Bunun ne kadar zor bir iş olduğunu anlamak için hesap makinenizi de kullanarak Örneğin, 431.909 sayısının iki asal çarpanı bulmaya çalışın.