Bir Çemberde Çevre Açının Ölçüsünün Gördüğü Yayın Ölçüsünün Yarısına Eşit Olduğunun İspatı

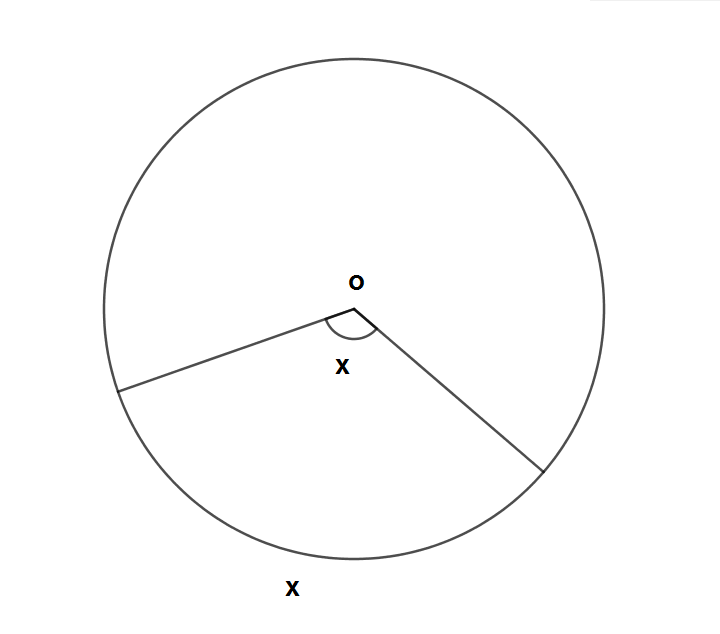
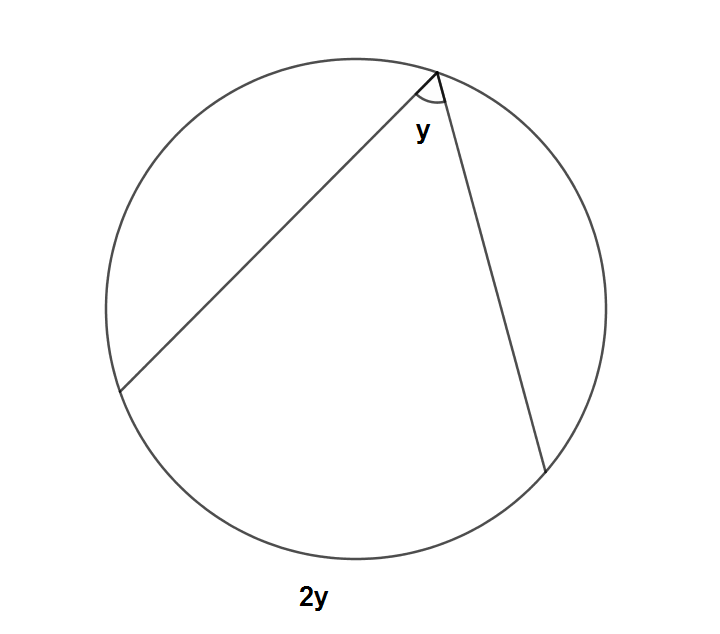
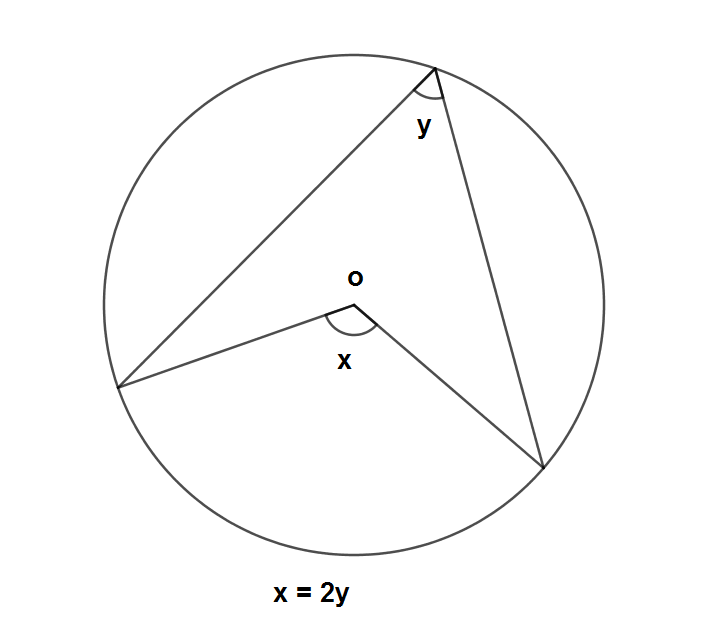
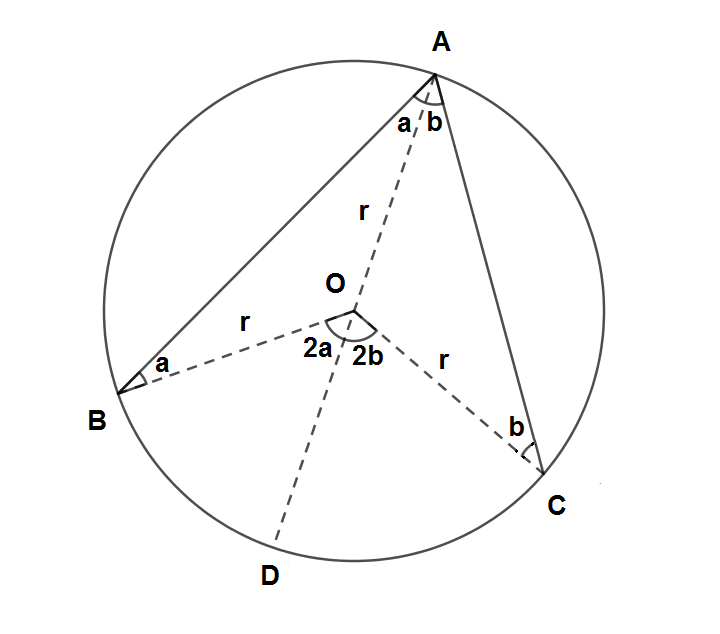
Bir çemberde çevre açının ölçüsünün gördüğü yayın ölçüsünün yarısına eşit olduğunu aşağıdaki şekildeki gibi ispatlayabiliriz.

Yukarıdaki çemberde m(OAB) ölçüsü a olsun AOB üçgeni ikiz kenar bir üçgen olduğuna göre (OA = OB) m(ABO) = m(OAB) = a olur.

m(BOD) = m(OAB) + m(ABO) = a+a = 2a olur.

m(OAC) ölçüsü b olsun AOC üçgeni ikiz kenar bir üçgen olduğuna göre (OA = OC)

m(OAC) = m(ACO) = b olur.

m(COD) = m(OAC) + m(ACO) = b+b = 2b olur.

m(BDC) = m(BOC) = 2a+2b = 2.(a+b)

m(BAC) = a+b

m(BAC)/m(BDC) = (a+b)/2.(a+b) = 1/2 olduğuna göre çevre açının ölçüsü gördüğü yayın ölçüsünün yarısına eşittir.