Fonksiyonların Grafikleri

Fonksiyon Nedir?

A ≠ Ø ve B ≠ Ø olmak üzere, A'dan B'ye bir β bağıntısı verilmiş olsun. A’nın her elemanı B’nin elemanlarıyla bir ve yalnız bir kere eşleniyorsa bu bağıntıya fonksiyon denir.



a ∈ A ve b ∈ B olmak üzere, A’dan B’ye bir f fonksiyonu f: A → B veya a → f(a) = b şeklinde gösterilir. A’ya fonksiyonun tanım kümesi, B ye ise değer kümesi denir.



Yukarıdaki bağıntıyı reel sayılar kümesi için yazarsak f: R → R veya x → f(x) = y şeklinde gösterilir. Bir bağıntının bir noktada fonksiyon olabilmesi için o noktadaki tanım kümesi değerin mutlaka bir değer kümesi değeri ile eşlenmesi gerekir; eğer eşlenmiyorsa fonksiyon bu noktada tanımlı değildir.



A. Birinci Dereceden Fonksiyonların Grafikleri

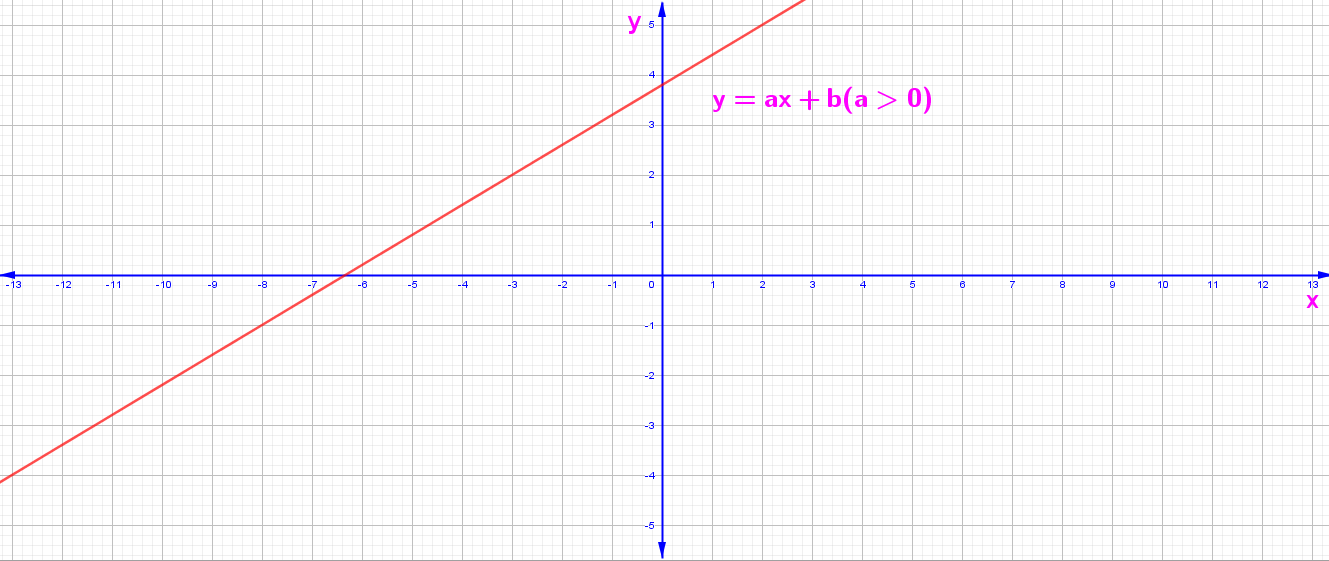
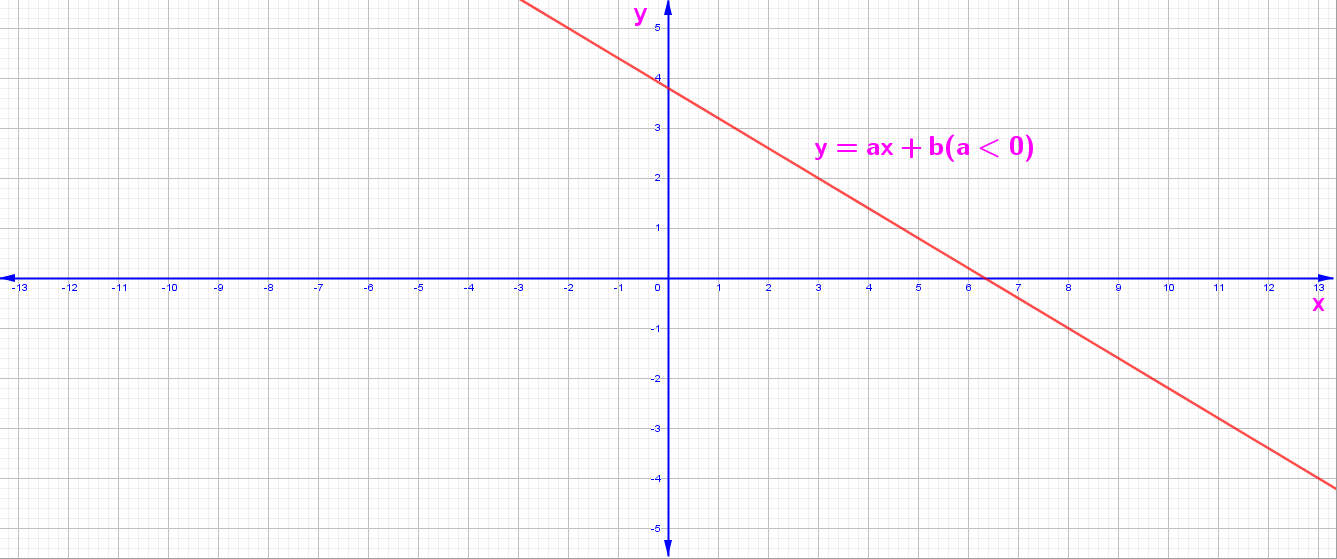
y = f(x) = ax + b Fonksiyonunun Grafiği

1. a > 0 İçin





2. a < 0 İçin





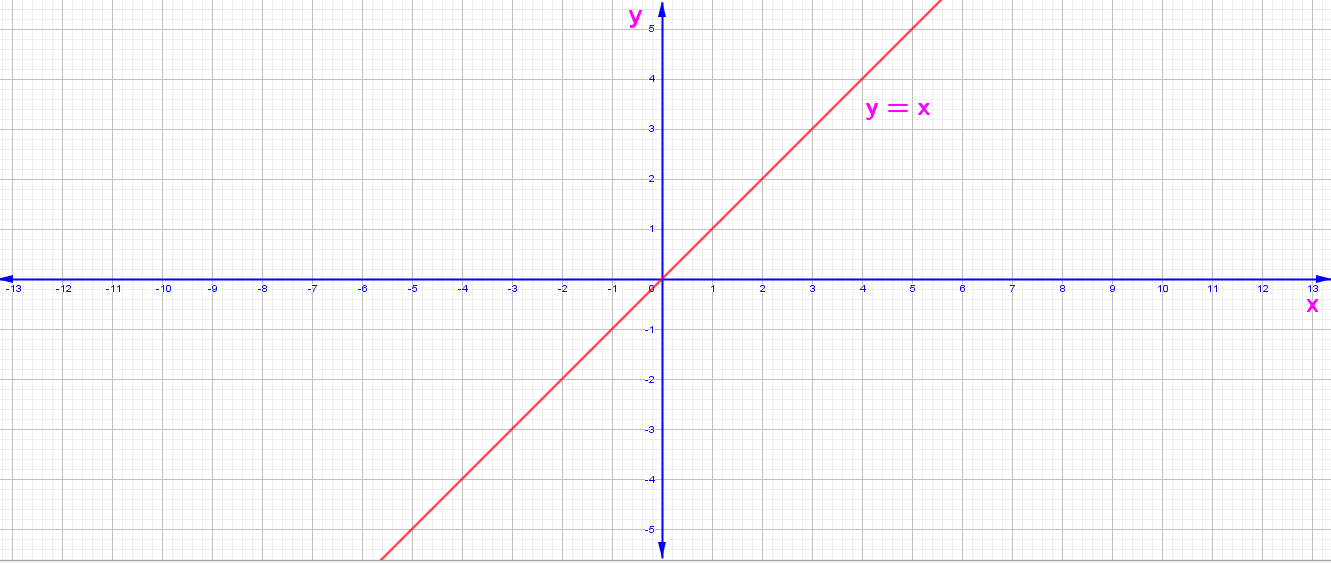
3. y = f(x) = x





B. İkinci Dereceden Fonksiyonların Grafikleri

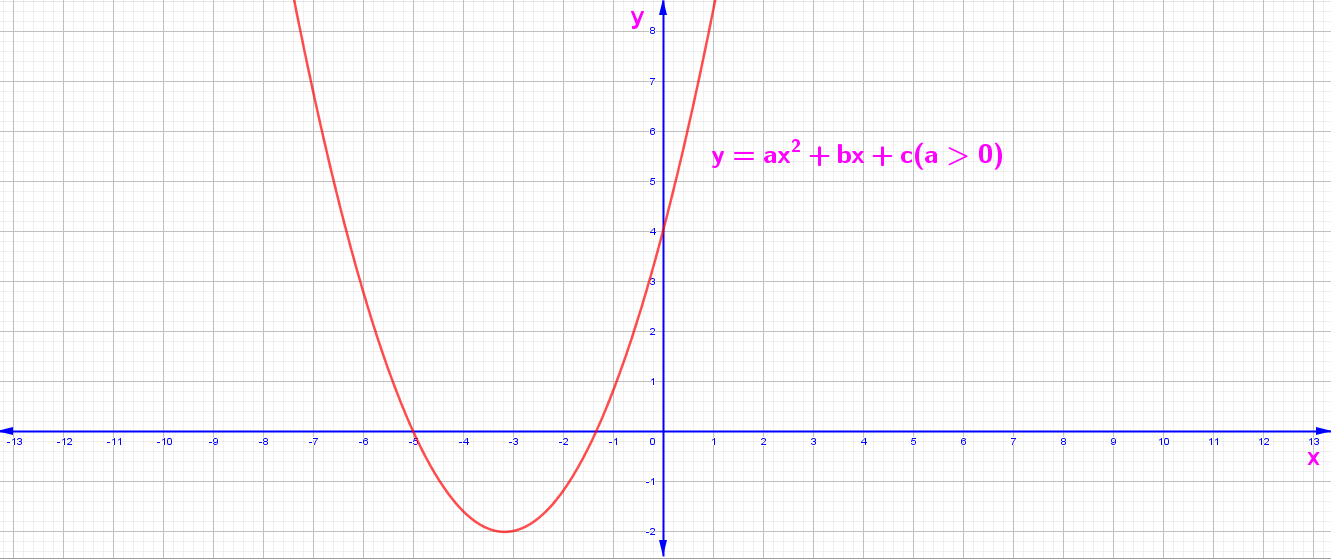
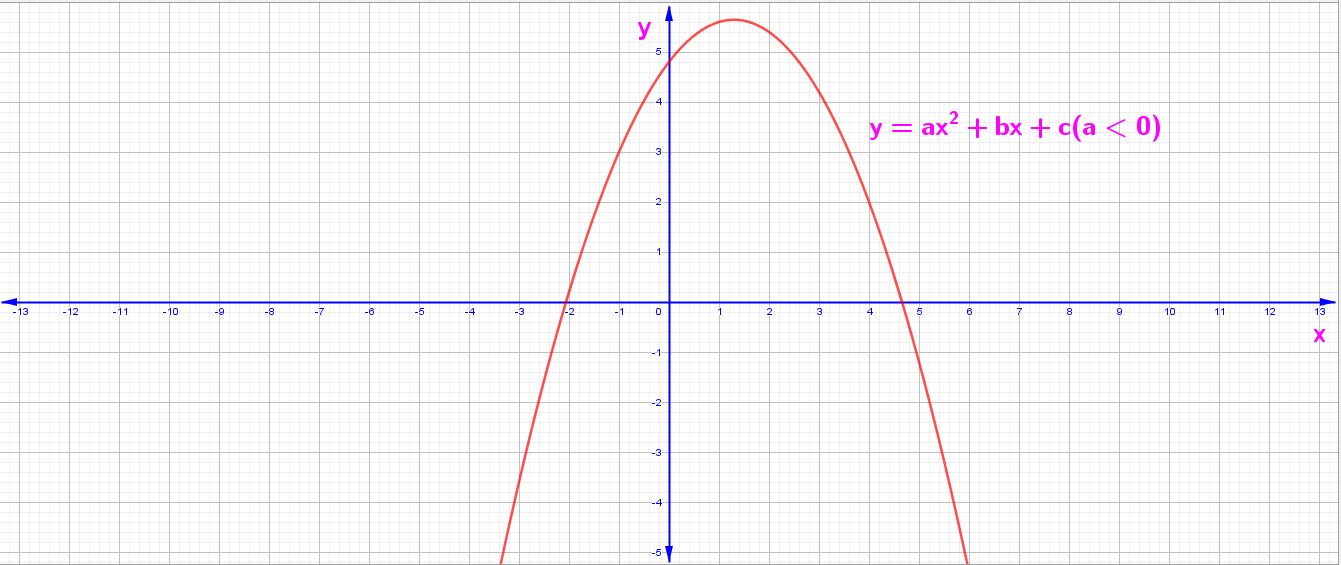
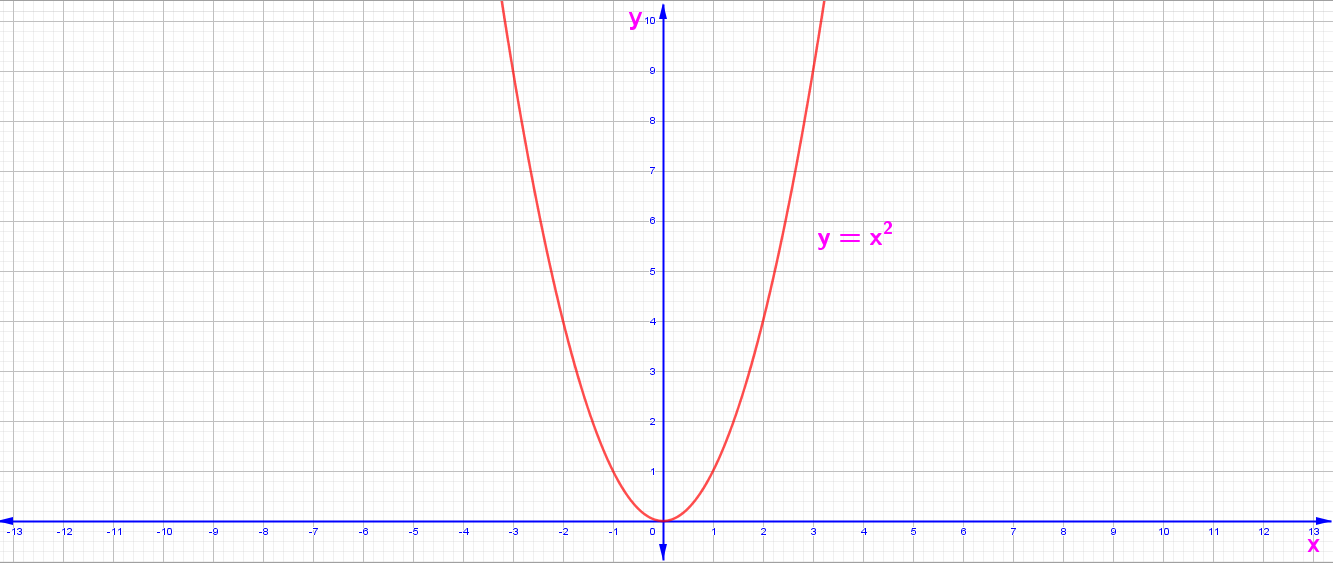
y = f(x) = ax² + bx + c Fonksiyonunun Grafiği

1. a > 0 İçin





2. a < 0 İçin





3. y = f(x) = x²





C. Üçüncü Dereceden Fonksiyonların Grafikleri

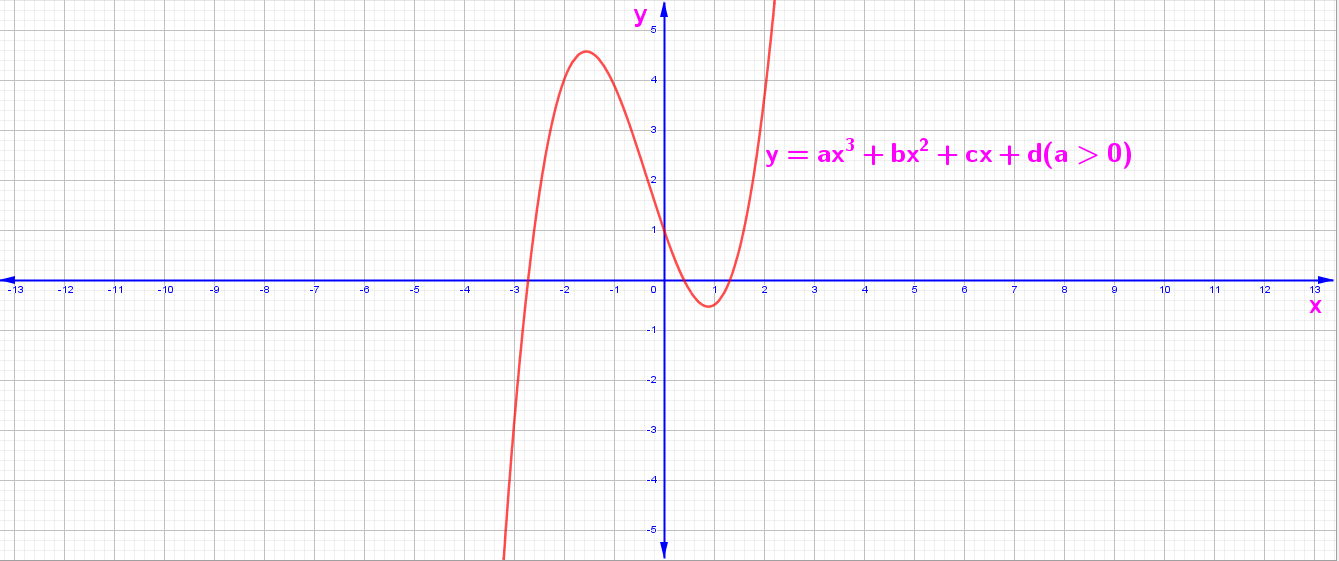
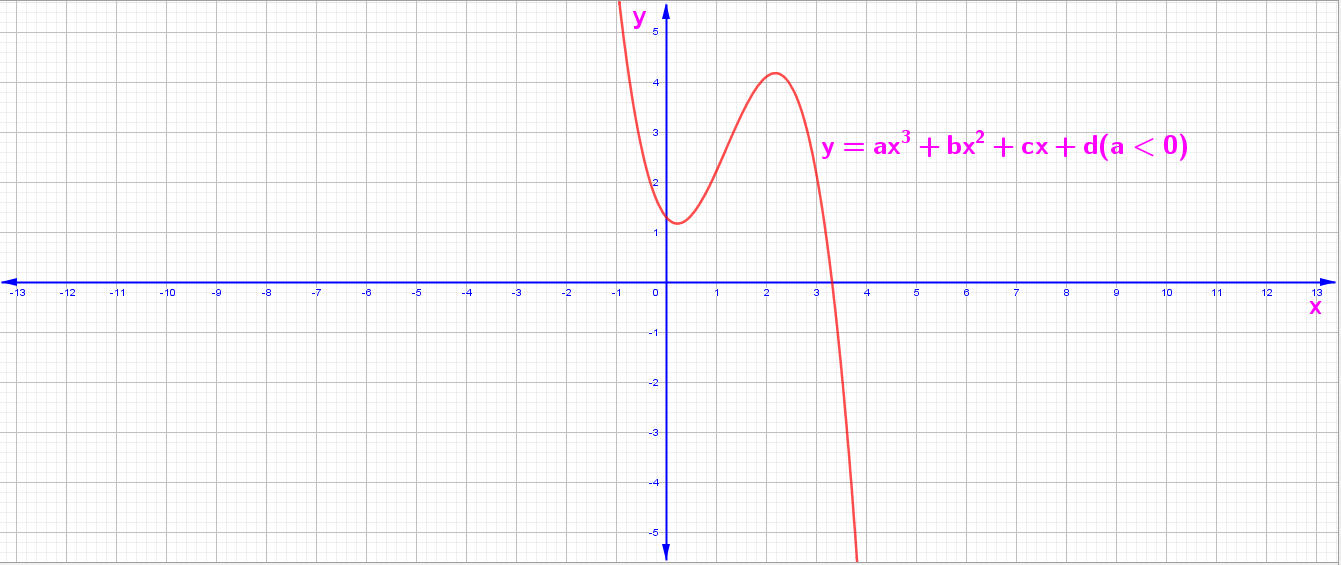
y = f(x) = ax³ + bx² + cx + d Fonksiyonunun Grafiği

1. a > 0 İçin





2. a < 0 İçin





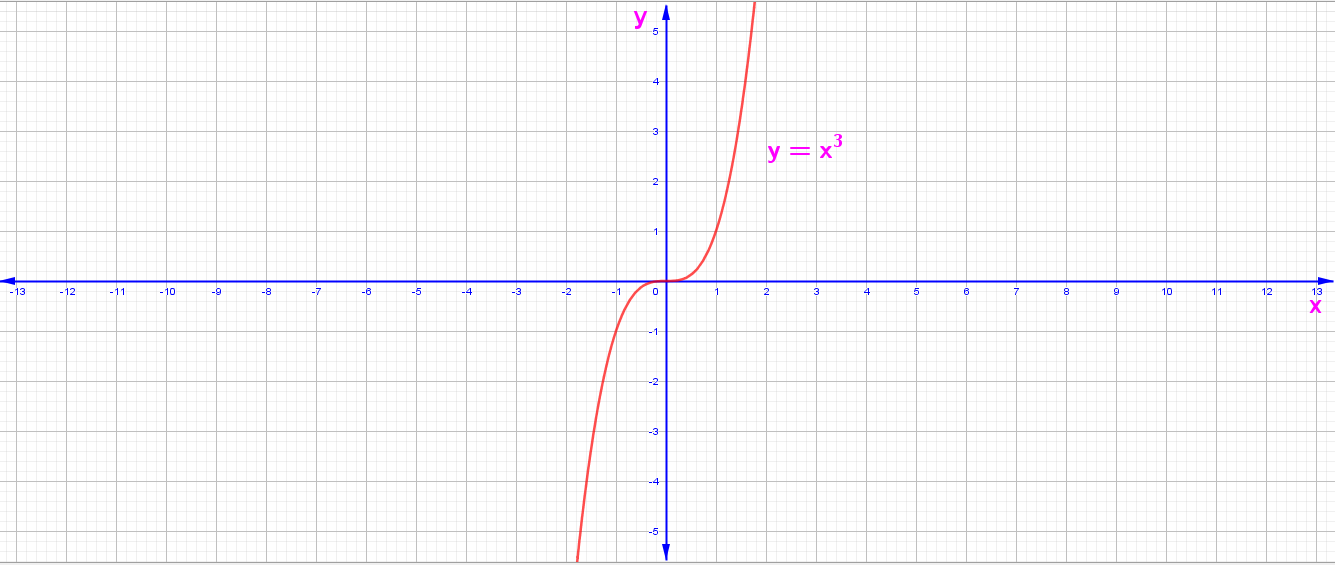
3. y = f(x) = x³





D. Rasyonel Fonksiyonların Grafikleri

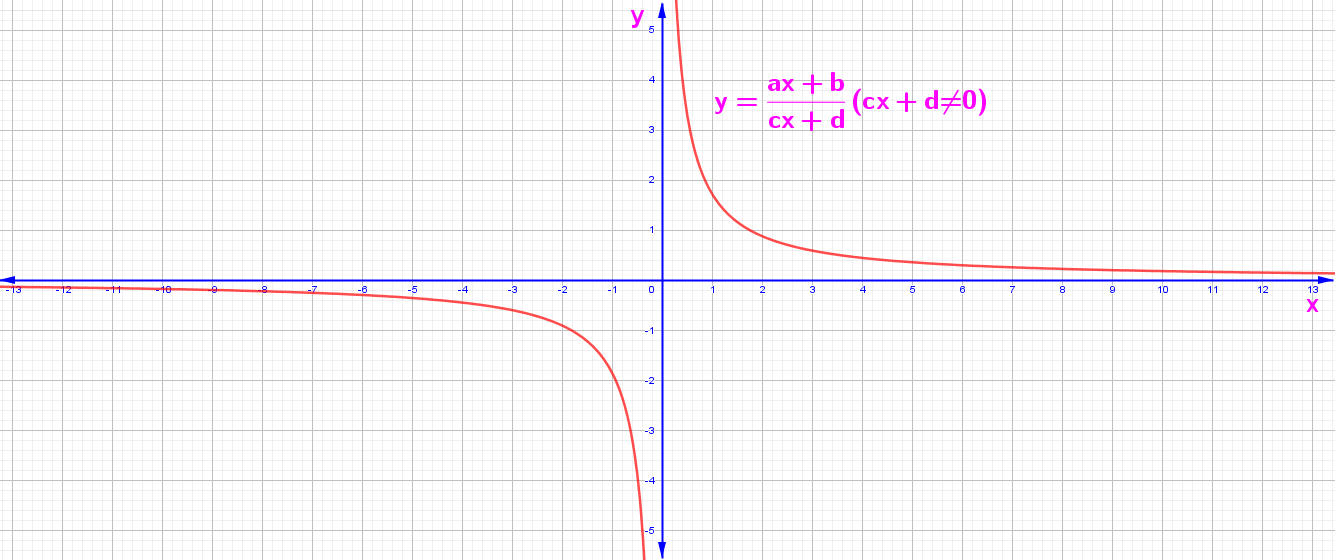
1. y = f(x) = (ax + b) / (cx + d) (cx + d ≠ 0)





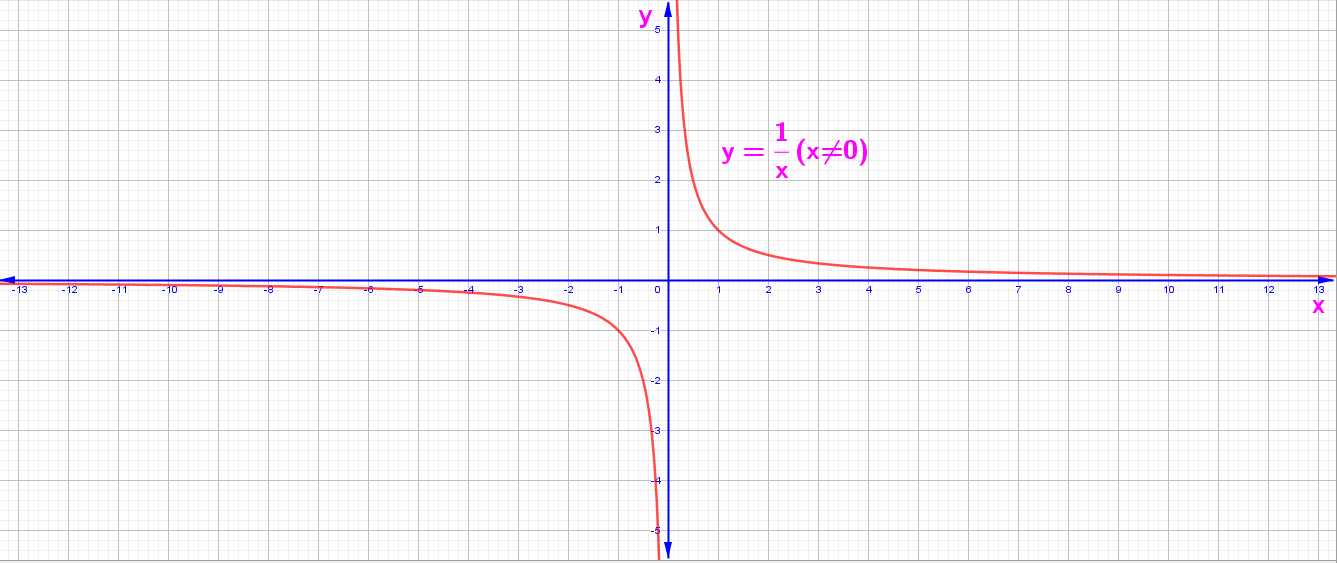
2. y = f(x) =1 / x (x ≠ 0)





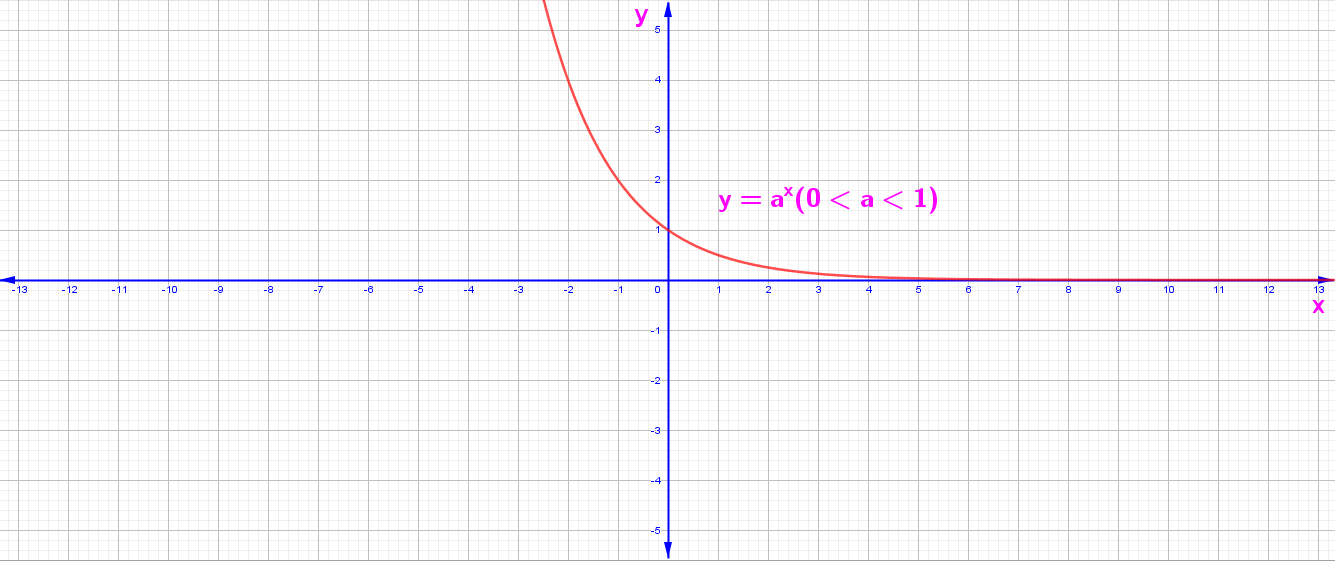
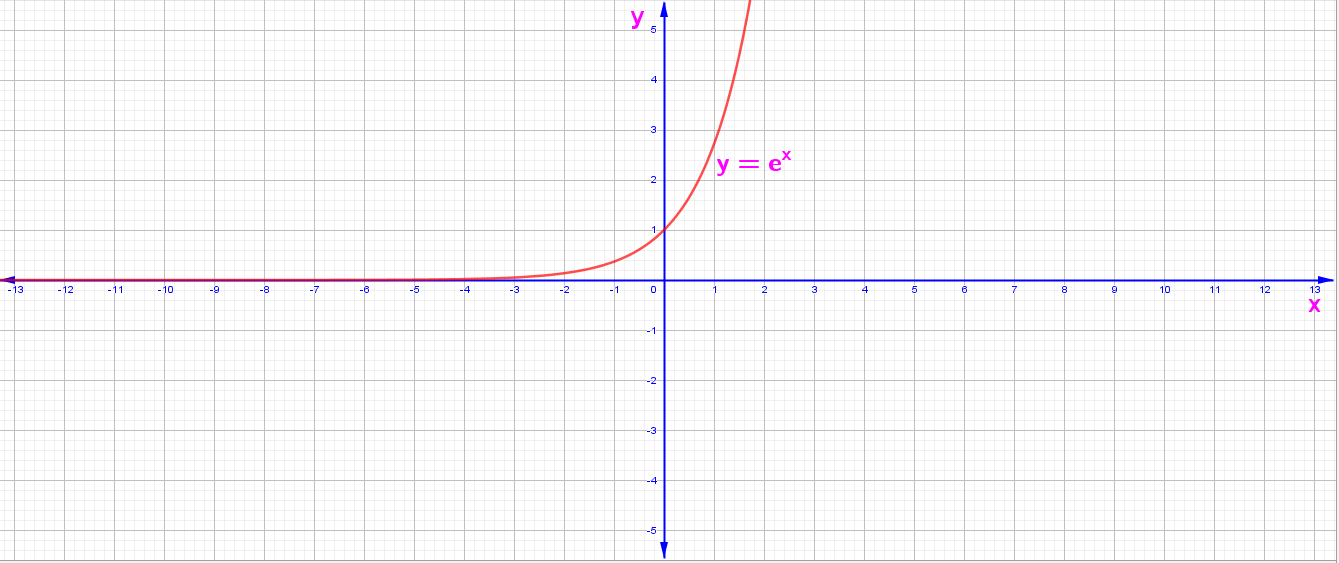
E. Üstel Fonksiyonların Grafikleri

y = f(x) = aˣ Fonksiyonun Grafiği

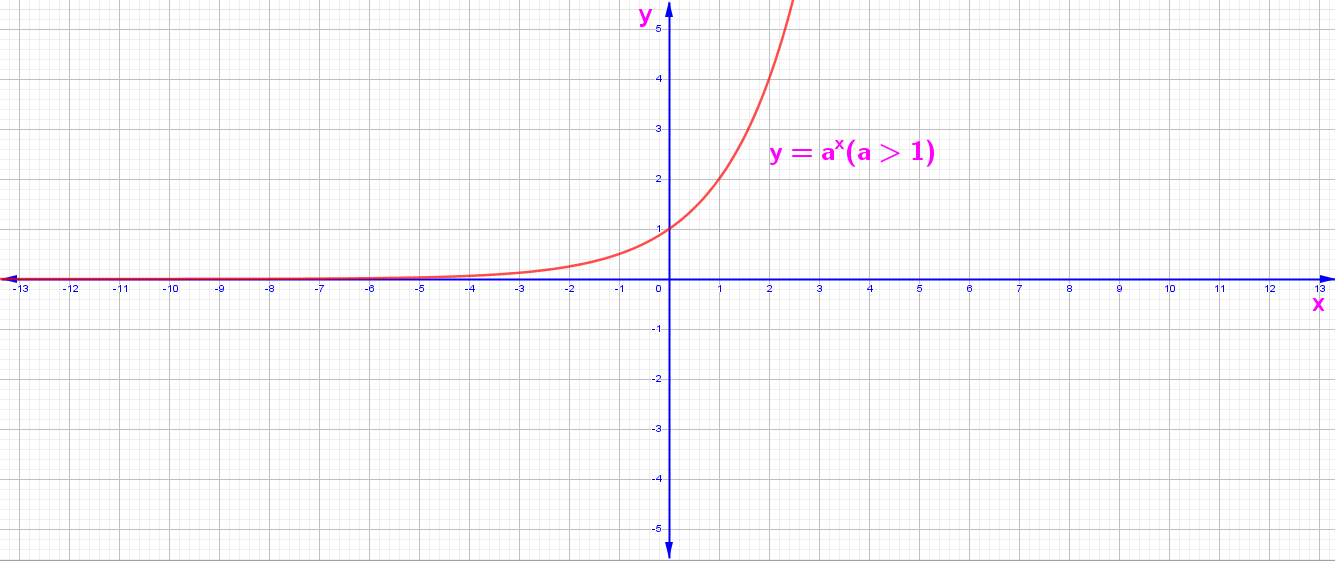
1. a > 0 İçin





2. 0 < a < 1 İçin





3. y = f(x) = eˣ





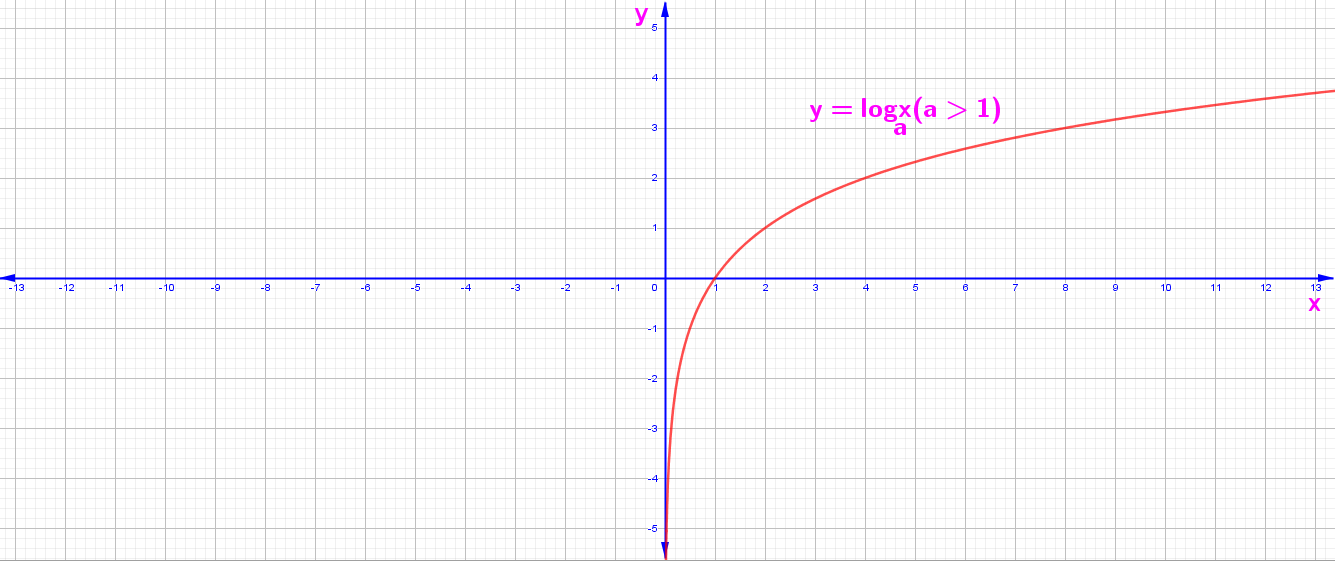
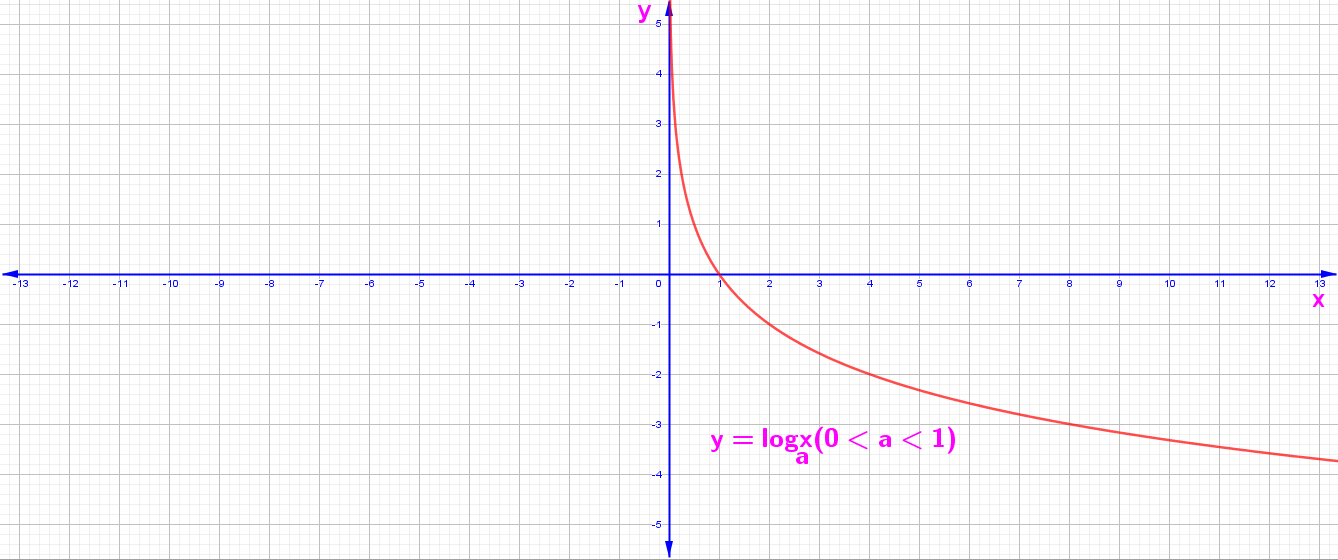
F. Logaritmik Fonksiyonların Grafikleri

y = f(x) = Loga x Fonksiyonun Grafiği

1. a > 1 İçin





2. 0 < a < 1 İçin





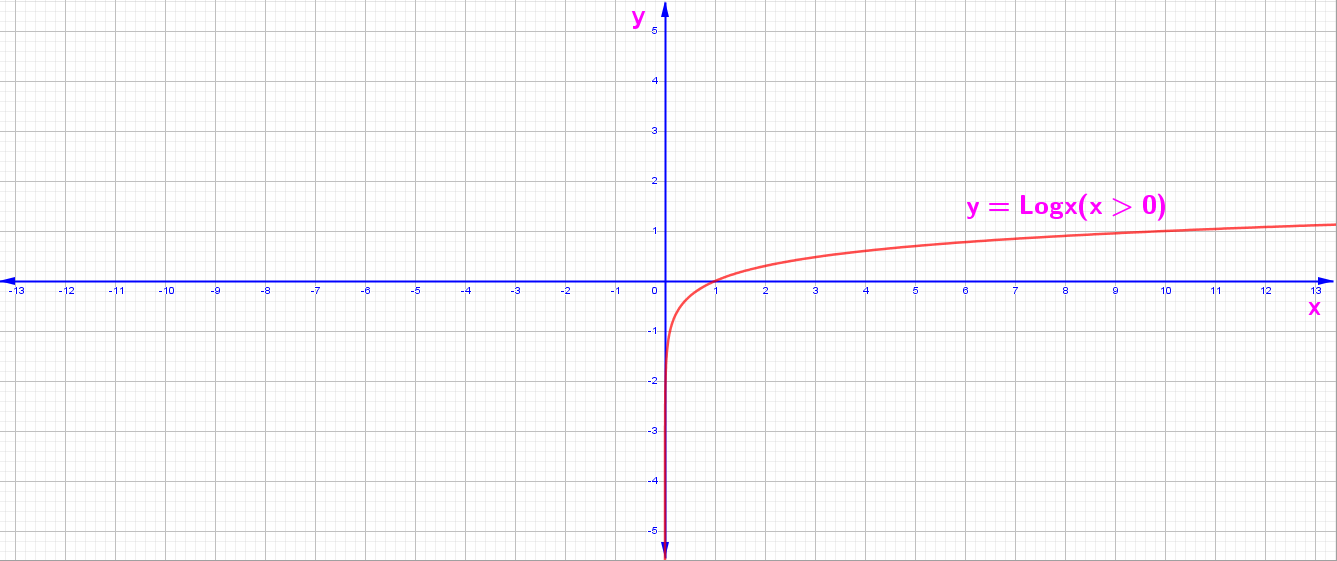
3. y = f(x) = Logx (x > 0)





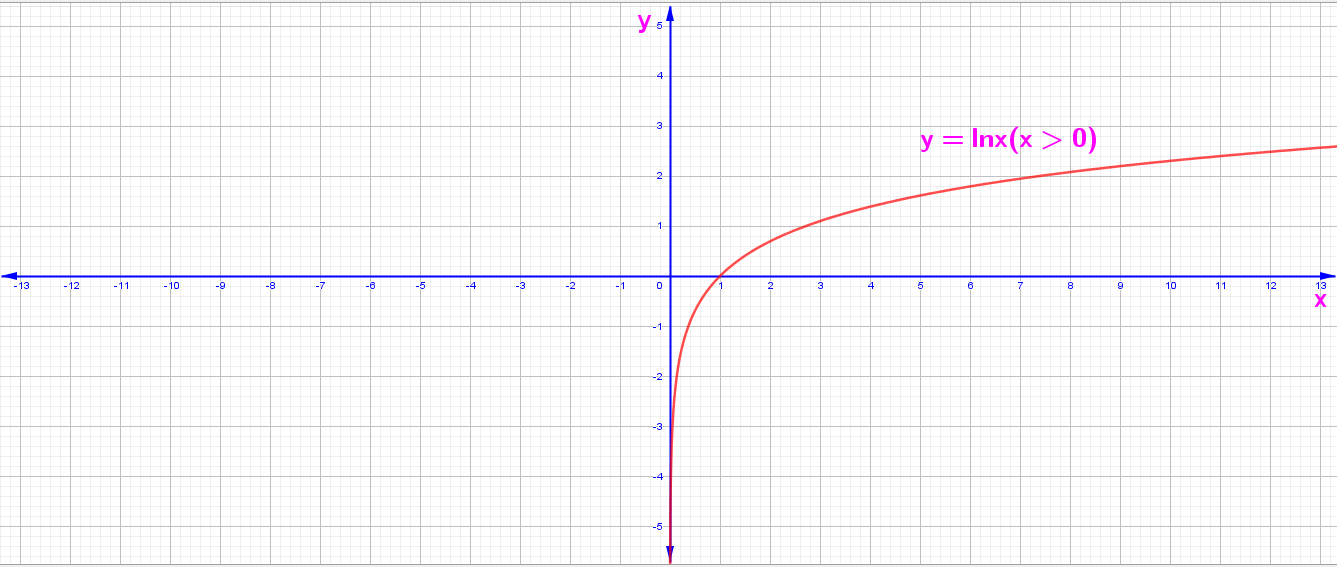
4. y = f(x) = Lnx (x > 0)





G. Kareköklü Fonksiyonların Grafiği

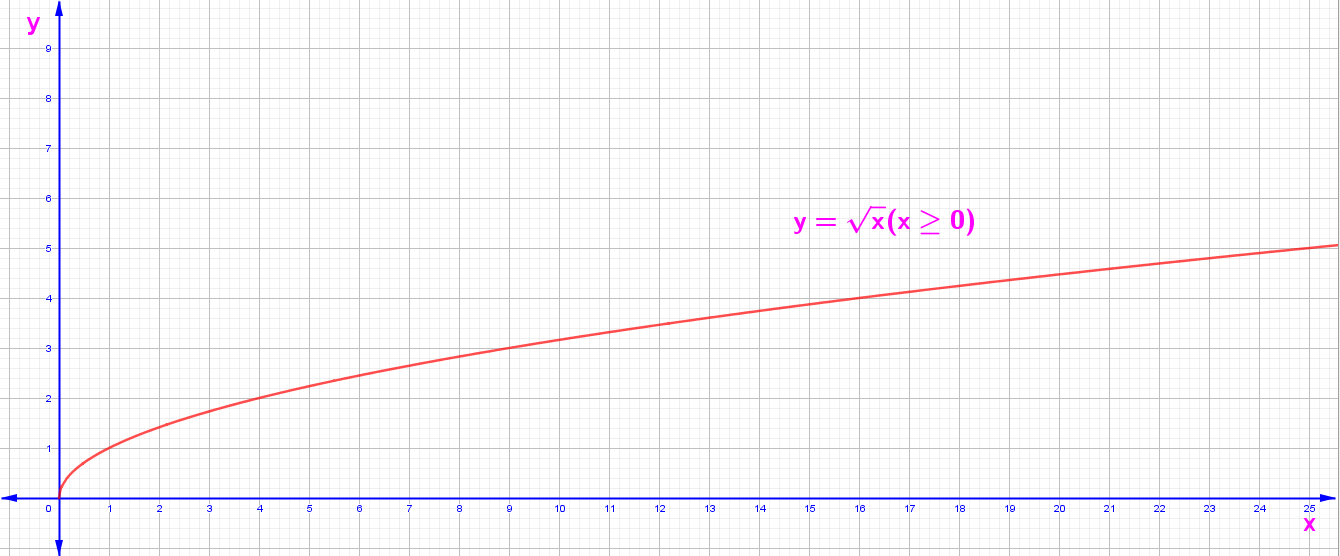
y = f(x) = √x (x ≥ 0)





H. Sabit Fonksiyonun Grafiği

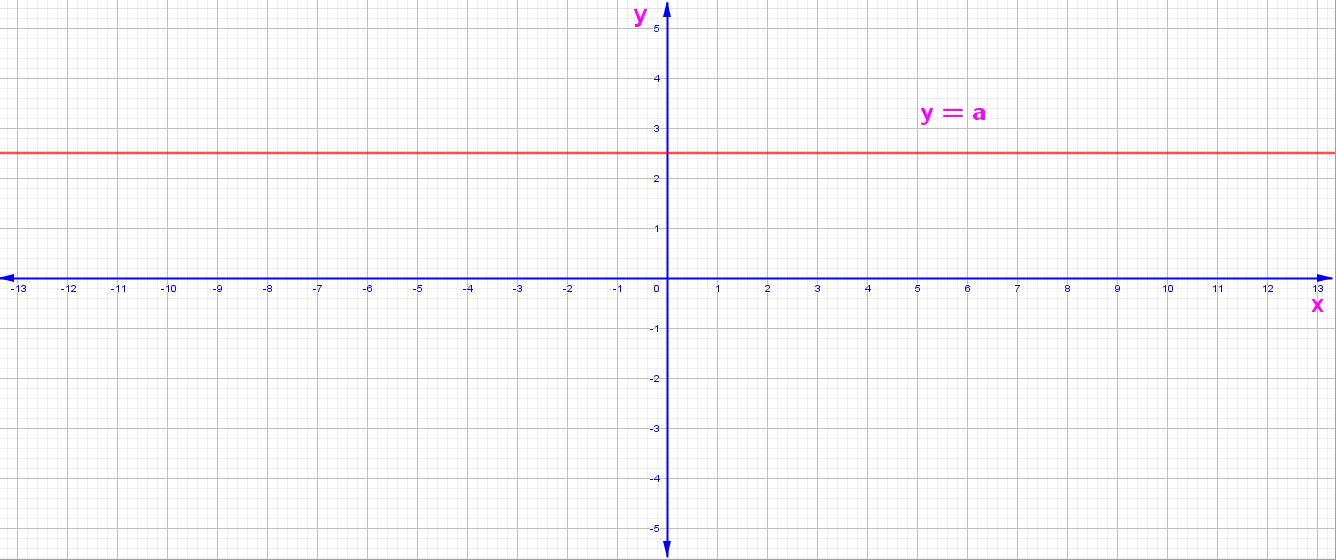
y = f(x) = a





I. Özel Tanımlı Fonksiyonların Grafiği

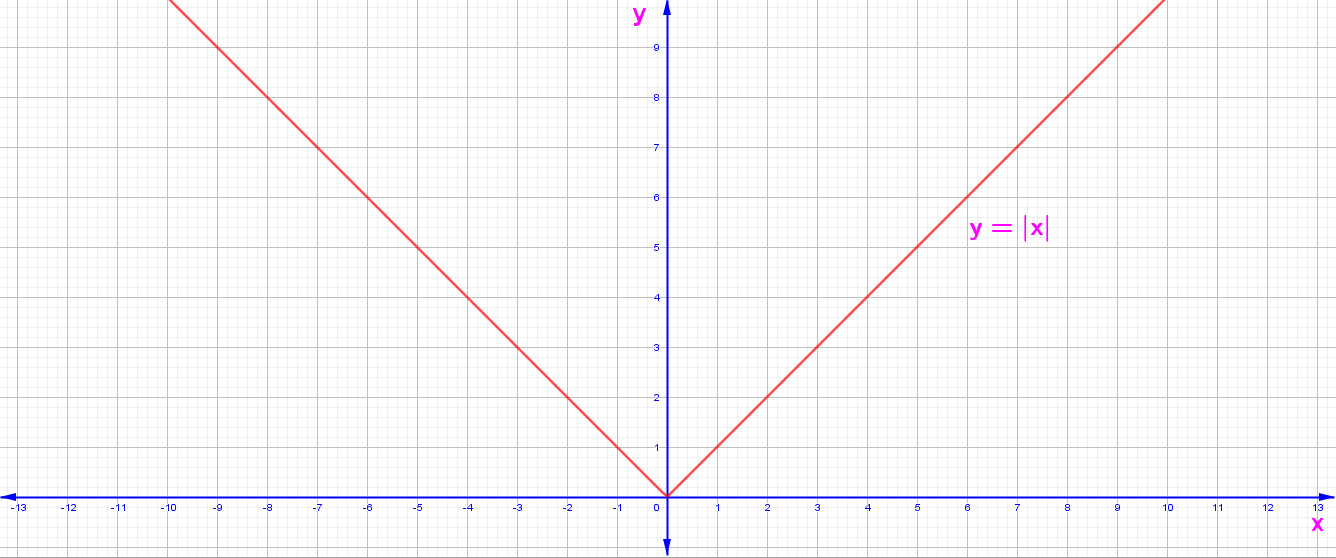
1. y = f(x) = |x| (Mutlak Değer Fonksiyonunun Grafiği)





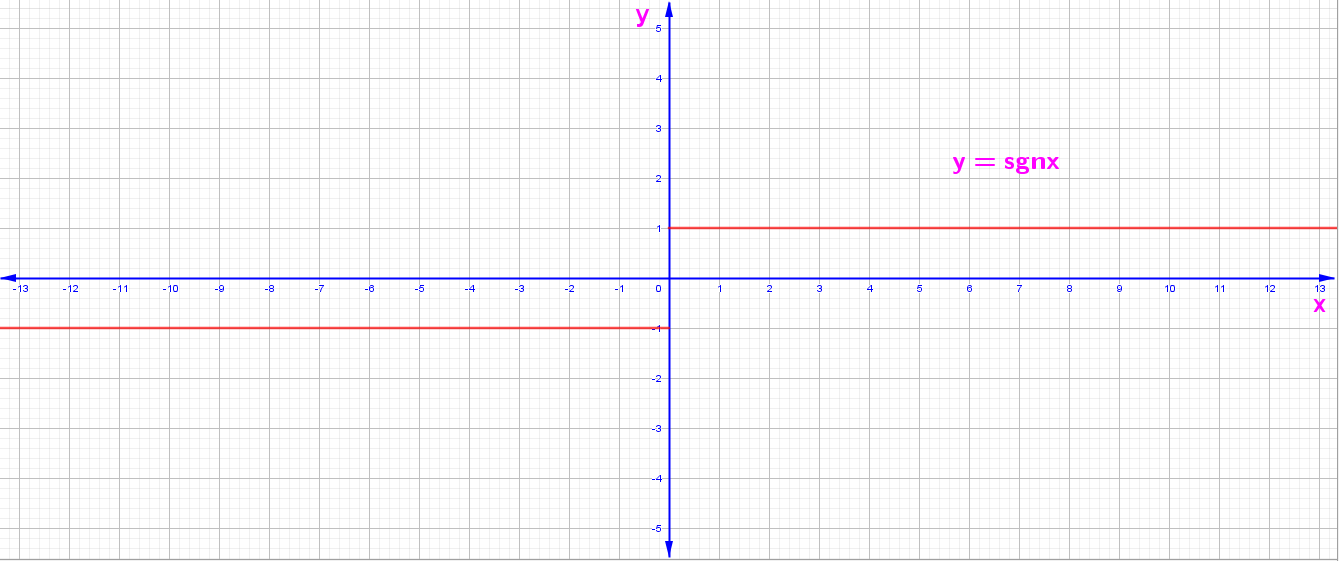
2. y = f(x) = Sgnx (İşaret Fonksiyonun Grafiği)





J. Trigonometrik Fonksiyonların Grafikleri

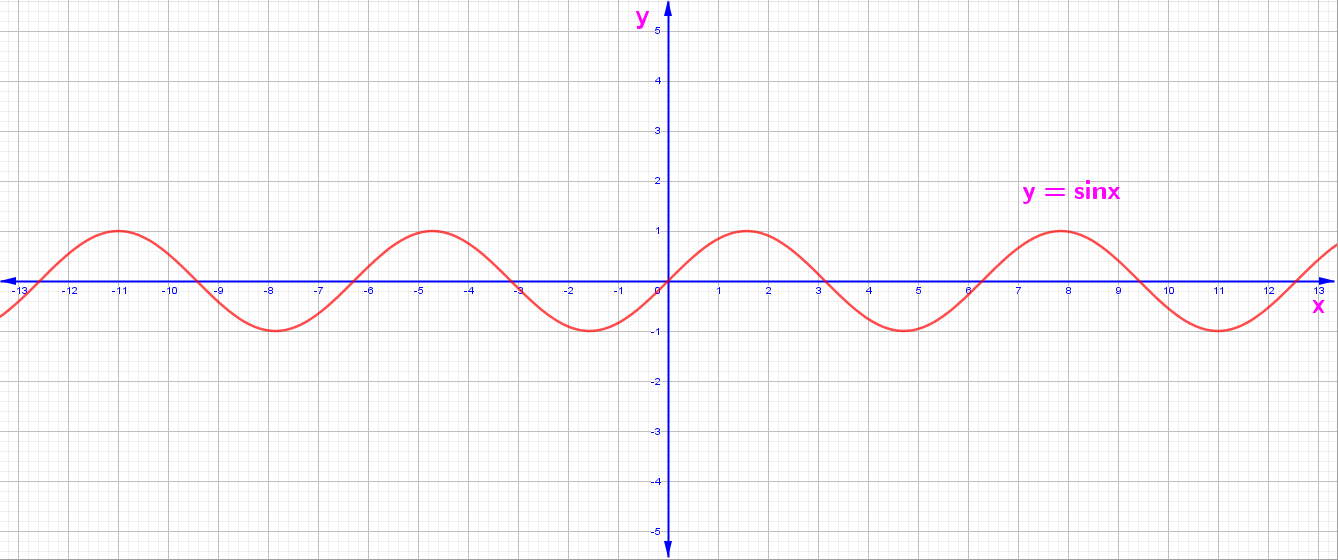
1. y = f(x) = Sinx





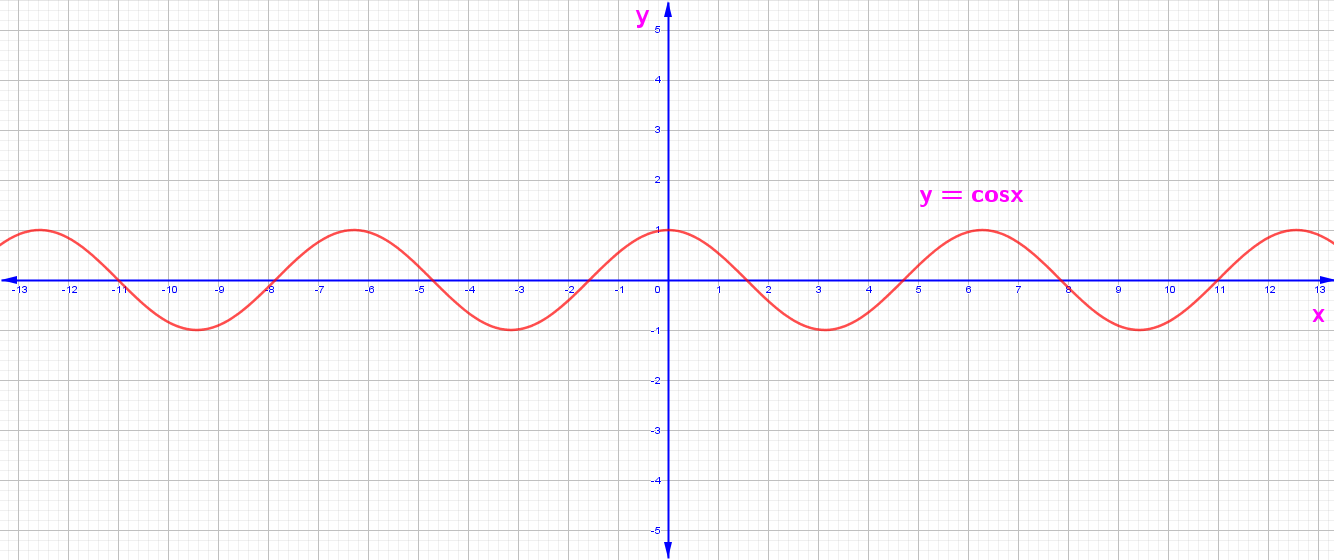
2. y = f(x) = Cosx





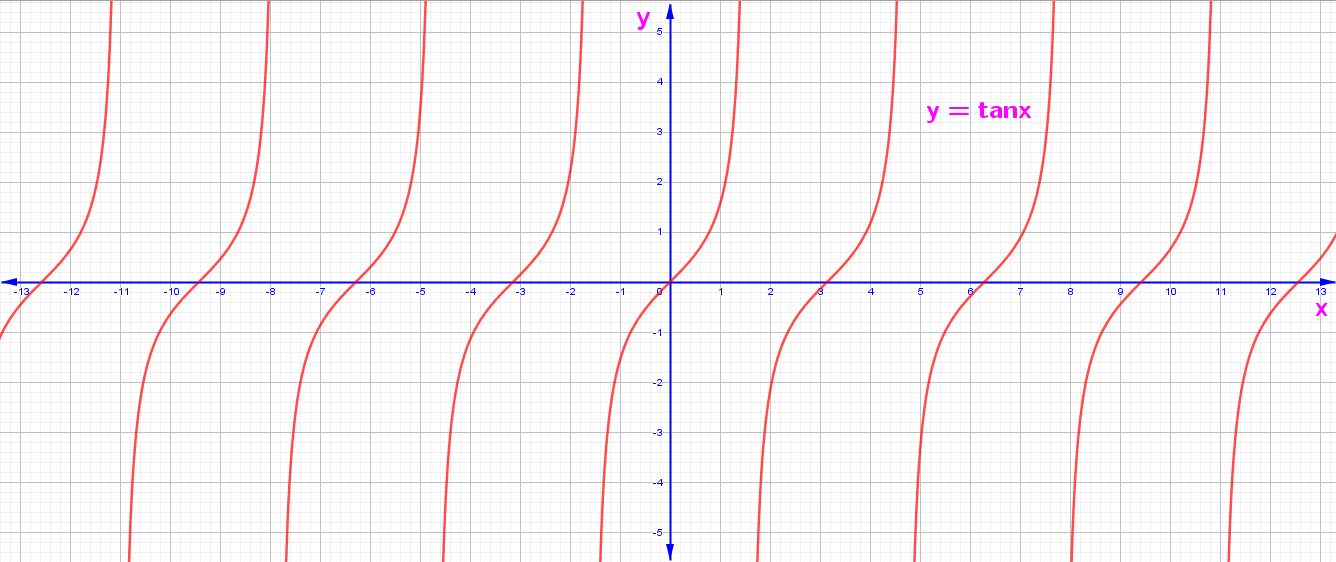
3. y = f(x) = Tanx





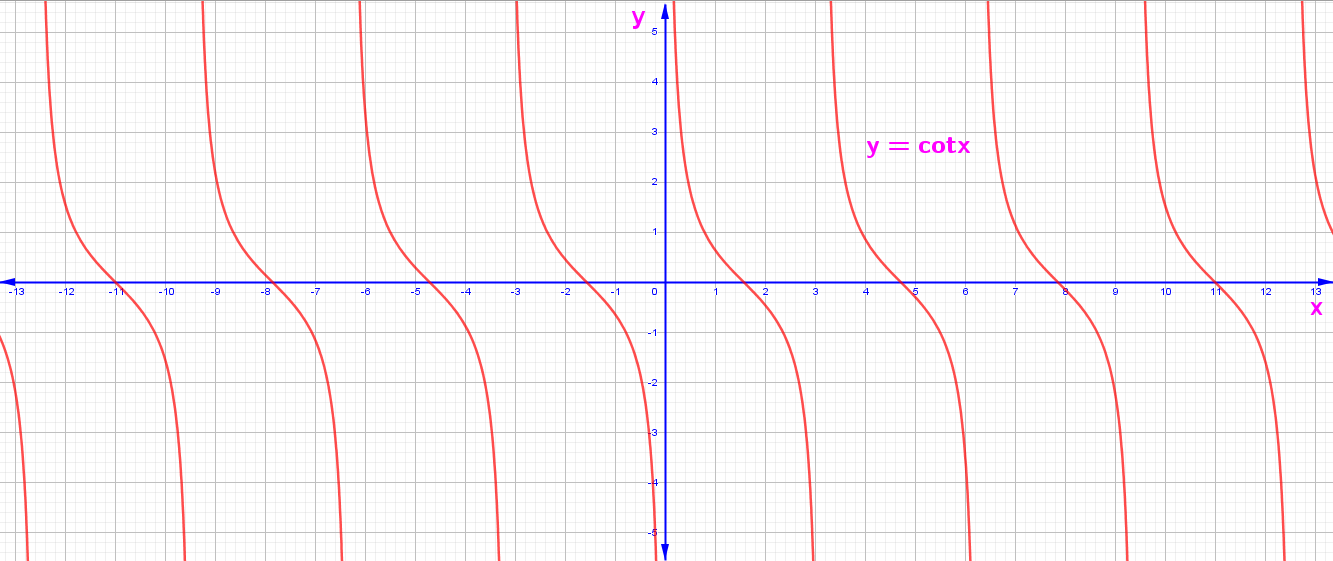
4. y = f(x) = Cotx