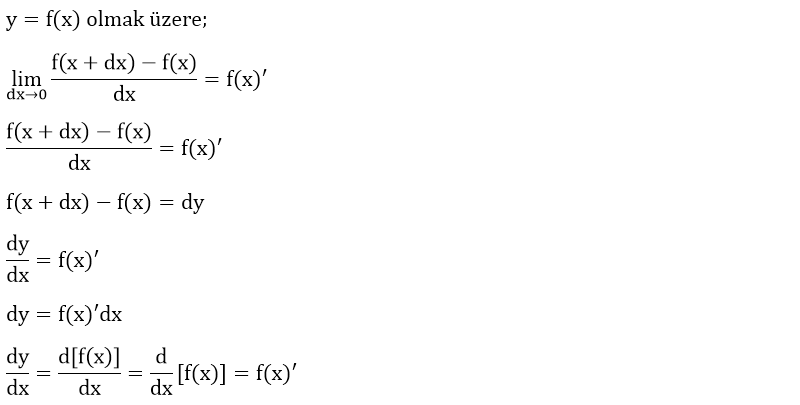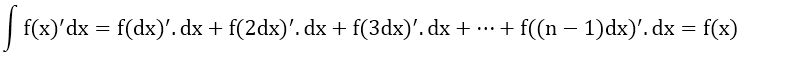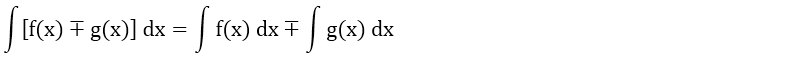İntegral Alma Kuralları

İntegral Nedir?

Türevi (diferansiyeli) alınmış bir fonksiyonun kendisini bulma işlemidir. Belirli ve belirsiz integral olmak üzere ikiye ayrılır.

Belirsiz İntegral

Belirsiz integral de integralin sınırları kesin olarak belirlenmemiştir. Belirsiz integral türevi alınmış bir fonksiyonun kendisini bulmamızı sağlar.

∫ : İntegral işareti (sembolü)

f(x)' : f(x) fonksiyonunun türevi

dx : Sonsuz küçüklükteki x genişliği

c : İntegral sabiti.

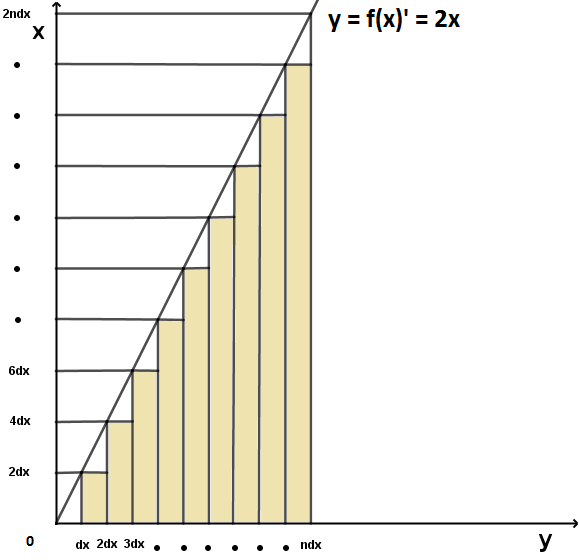
dx = x/n olsun. Buradaki n çok büyük (sonsuz büyüklükte) bir sayı olup dx ise çok küçük (sonsuz küçüklükte) bir sayıdır.

Yukarıdaki şekildeki y = f(x) = 2x fonksiyonunun eğrisinin altında kalan sonsuz sayıdaki (çokluktaki) dikdörtgenlerin alanlarını teker teker toplayalım.

1. Dikdörtgenin Alanı = 2dx . (2dx - dx) = 2dx . dx = 2dx²

2. Dikdörtgenin Alanı = 4dx . (3dx - 2dx) = 4dx . dx = 4dx²

3. Dikdörtgenin Alanı = 6dx . (4dx - 3dx) = 6dx . dx = 6dx²

. . .

(n-1). Dikdörtgenin Alanı = 2(n-1)dx . (ndx - (n-1)dx) = 2(n-1)dx . dx = 2(n-1)dx²

Toplam Alan = 2dx² + 4dx² + 6dx² + . . . + 2(n-1)dx²

Toplam Alan = 2dx² . [1 + 2 + 3 + . . . + (n-1)]

1 + 2 + 3 + . . . + n = n . (n+1) / 2 olduğuna göre;

1 + 2 + 3 + . . . + (n-1) = (n-1) . (n-1+1) = (n-1) . n / 2 olur.

Toplam Alan = 2dx² . (n-1) . n / 2 = 2dx² . (n²-n) / 2

dx = x/n

dx² = (x/n)²

dx² = x²/n² olur.

Toplam Alan = 2x² / n² . (n²-n) / 2

Toplam Alan = x² . (n²-n) / n²

Toplam Alan = x² . n² . (1-1/n) / n²

Toplam Alan = x² . (1-1/n)

Toplam Alan = x² . (1-0)

Toplam Alan = x² . 1

Toplam Alan = x² olur.

İntegral Alma Kuralları

1. Sabit Sayının İntegrali

Sabit bir sayının integrali alınırken yanına x getirilir.

2. Üslü Fonksiyonun İntegrali

Üs bir artırılır ve oluşan yeni üslü ifade paya üs ise paydaya yazılır. (n ≠ -1)

3. 1 / x Fonksiyonunun İntegrali

1 / x Fonksiyonunun integrali lnx'e eşittir.

4. Önünde Sabit Bir Sayı Bulunan Fonksiyonun İntegrali

Önünde sabit bir sayı bulunan bir fonksiyonun integrali alınırken sabit sayı integral dışarısına çıkarılarak yalnızca fonksiyonun integrali de alınabilir.

5. Toplam veya Fark Şeklindeki Fonksiyonların İntegrali

Toplam veya fark şeklindeki fonksiyonların integrali, fonksiyonların ayrı ayrı integrali alındıktan sonraki toplam veya farkına eşittir.

6. Üstel Fonksiyonların İntegrali

Üstel fonksiyonların integrali aşağıdaki şekildeki gibidir. (a > 0)

7. Logaritmik Fonksiyonların İntegrali

Logaritmik fonksiyonların integrali aşağıdaki şekildeki gibidir.

8. Trigonometrik Fonksiyonların İntegrali

Trigonometrik fonksiyonların integrali aşağıdaki şekildeki gibidir.

9. Mutlak Değer Şeklindeki Fonksiyonların İntegrali

|x| Fonksiyonunun integrali aşağıdaki şekildeki gibidir.