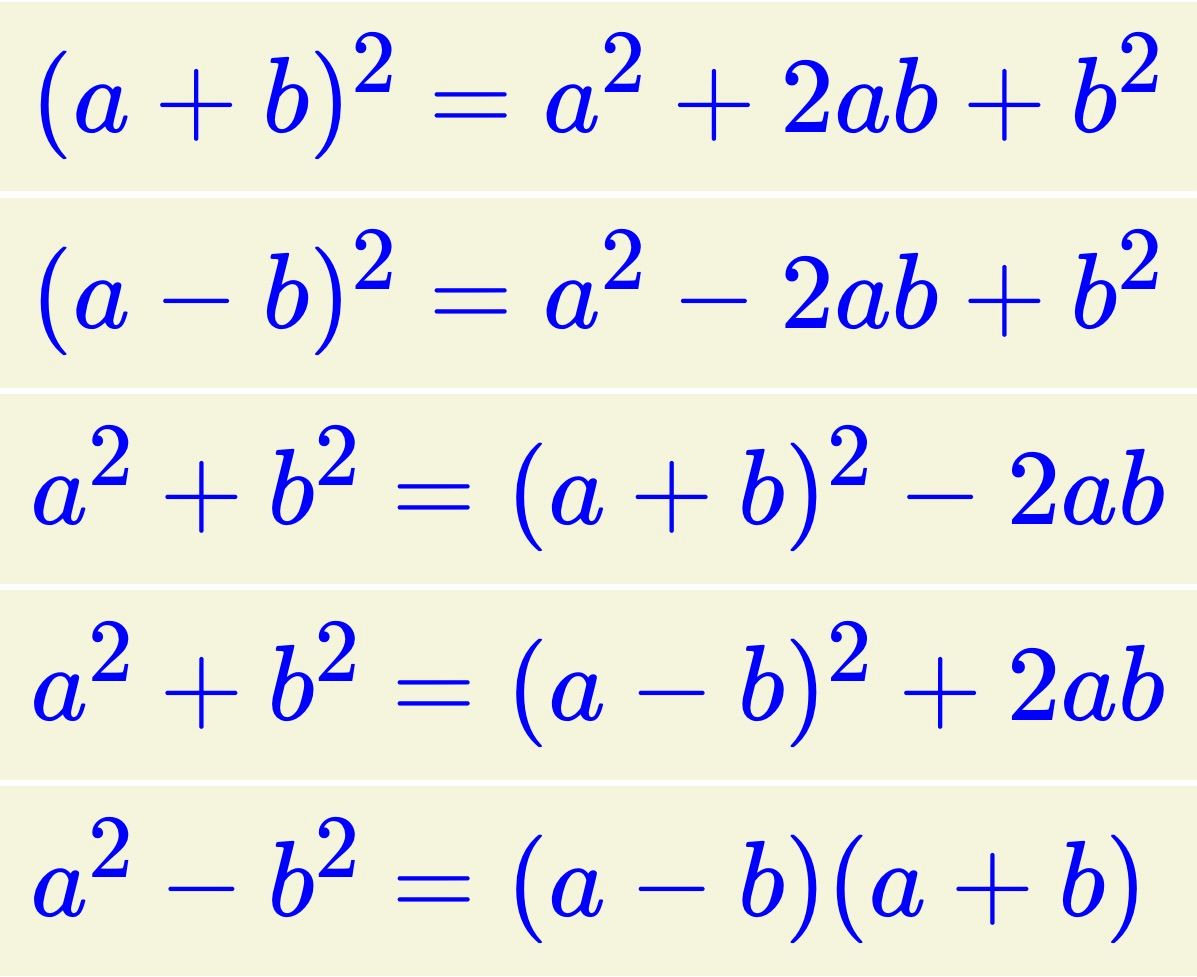Kare Açılımı

Kare Açılımı Formülleri

A. Tam Kare Açılımı

1. Tam Kare Toplamı Açılımı

Birincinin karesi artı birinci ile ikincinin çarpımının iki katı artı ikincinin karesi şeklindeki ifadeye Tam Kare Toplamı denir. Buna göre; (a + b)² = a² + 2.a.b + b²'dir. Bu ifadenin ispatını aşağıdaki şekildeki gibi gösterebiliriz.

1. İspatı

Çarpma işlemin toplama işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki özdeşliğin ispatını yapabiliriz.

$(a+b{)}^2=(a+b).(a+b)$

$(a+b{)}^2=(a+b).a+(a+b).b$

$(a+b{)}^2=a.(a+b)+b.(a+b)$

$(a+b{)}^2=a.a+a.b+b.a+b.b$

$(a+b{)}^2=a.a+a.b+a.b+b.b$

$(a+b{)}^2=a^2+2.a.b+b^2$

2. İspatı

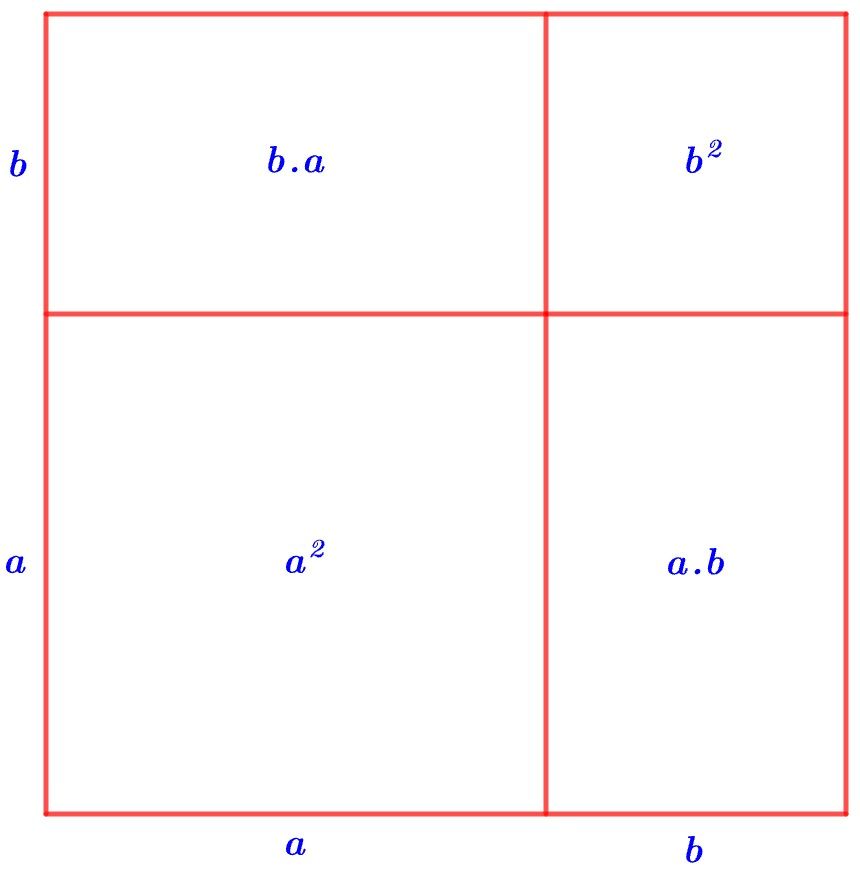
Geometrik şekil yardımıyla da yukarıdaki özdeşliğin ispatını yapabiliriz.

Yukarıdaki şekildeki büyük karenin alanı, iki küçük karenin alanı ile iki bir birine eş dikdörtgenin alanının toplamına eşittir. Buna göre;

$(a+b).(a+b)=b.a+a.a+a.b+b.b$

$(a+b{)}^2=b.a+a^2+a.b+b^2$

$(a+b{)}^2=a.b+a^2+a.b+b^2$

$(a+b{)}^2=a^2+2.a.b+b^2$ olur.

2. Tam Kare Farkı Açılımı

Birincinin karesi eksi birinci ile ikincinin çarpımının iki katı artı ikincinin karesi şeklindeki ifadeye Tam Kare Farkı denir. Buna göre; (a - b)² = a² - 2.a.b + b²'dir. Bu ifadenin ispatını aşağıdaki şekildeki gibi gösterebiliriz.

1. İspatı

Çarpma işlemin çıkarma işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki özdeşliğin ispatını yapabiliriz.

$(a-b{)}^2=(a-b).(a-b)$

$(a-b{)}^2=(a-b).a-(a-b).b$

$(a-b{)}^2=a.(a-b)-b.(a-b)$

$(a-b{)}^2=a.a-a.b-b.a-b.-b$

$(a-b{)}^2=a^2-a.b-b.a+b^2$

$(a-b{)}^2=a^2-a.b-a.b+b^2$

$(a-b{)}^2=a^2-2.a.b+b^2$

2. İspatı

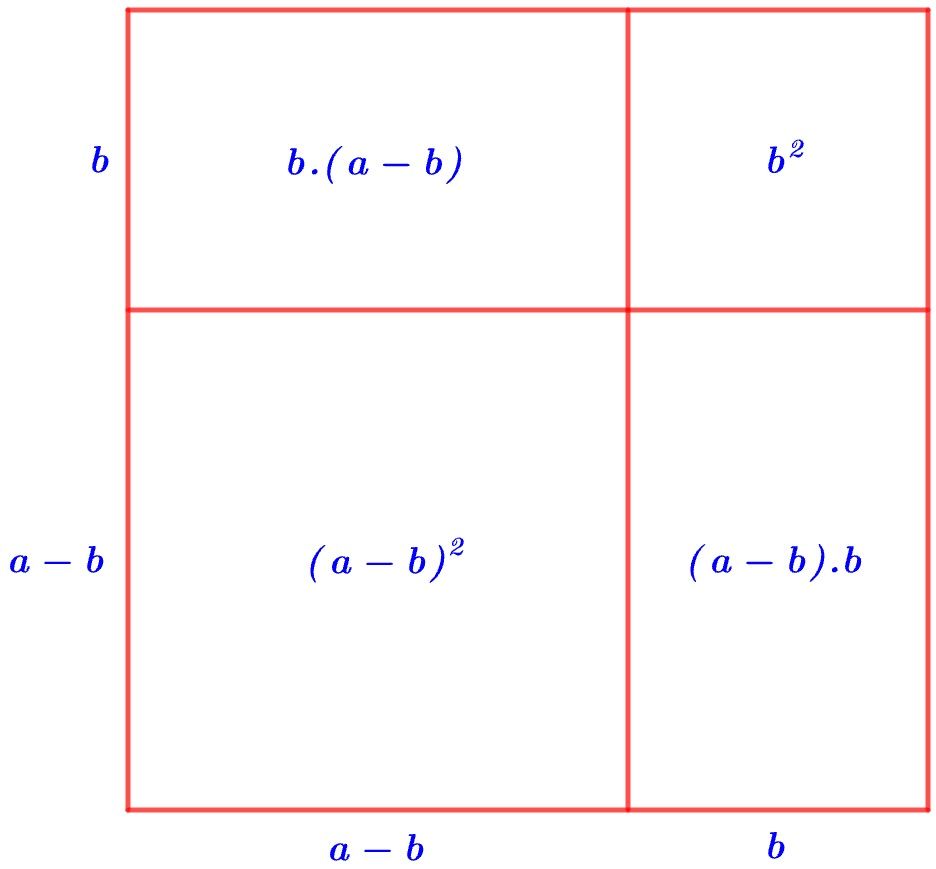
Geometrik şekil yardımıyla da yukarıdaki özdeşliğin ispatını yapabiliriz.

Yukarıdaki şekildeki büyük karenin alanı, iki küçük karenin alanı ile iki bir birine eş dikdörtgenin alanının toplamına eşittir. Buna göre;

$a^2=b.(a-b)+(a-b{)}^2+(a-b).b+b^2$

$a^2=b.(a-b)+(a-b{)}^2+b.(a-b)+b^2$

$a^2=b.a-b.b+(a-b{)}^2+b.a-b.b+b^2$

$a^2=b.a-b^2+(a-b{)}^2+b.a-\cancel{b^2}+\cancel{b^2}$

$a^2=b.a-b^2+(a-b{)}^2+b.a$

$a^2=2.b.a-b^2+(a-b{)}^2$

$a^2-2.b.a+b^2=(a-b{)}^2$

$a^2-2.a.b+b^2=(a-b{)}^2$ olur.

B. İki Kare Toplamı Açılımı

Birincinin karesi artı ikincinin karesi şeklindeki ifadeye İki Kare Toplamı denir.

1. a² + b² = (a + b)² - 2.a.b

2. a² + b² = (a - b)² + 2.a.b

C. İki Kare Farkı Açılımı

Birincinin karesi eksi ikincinin karesi şeklindeki ifadeye İki Kare Farkı denir. Buna göre; a² - b² = (a - b).(a + b)'dir. Bu ifadenin ispatını aşağıdaki şekildeki gibi gösterebiliriz.

1. İspatı

Çarpma işlemin toplama ve çıkarma işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki özdeşliğin ispatını yapabiliriz.

$(a-b).(a+b)=(a-b).a+(a-b).b$

$(a-b).(a+b)=a.(a-b)+b.(a-b)$

$(a-b).(a+b)=a.a-a.b+b.a-b.b$

$(a-b).(a+b)=a.a-\cancel{a.b}+\cancel{a.b}-b.b$

$(a-b).(a+b)=a.a-b.b$

$(a-b).(a+b)=a^2-b^2$

2. İspatı

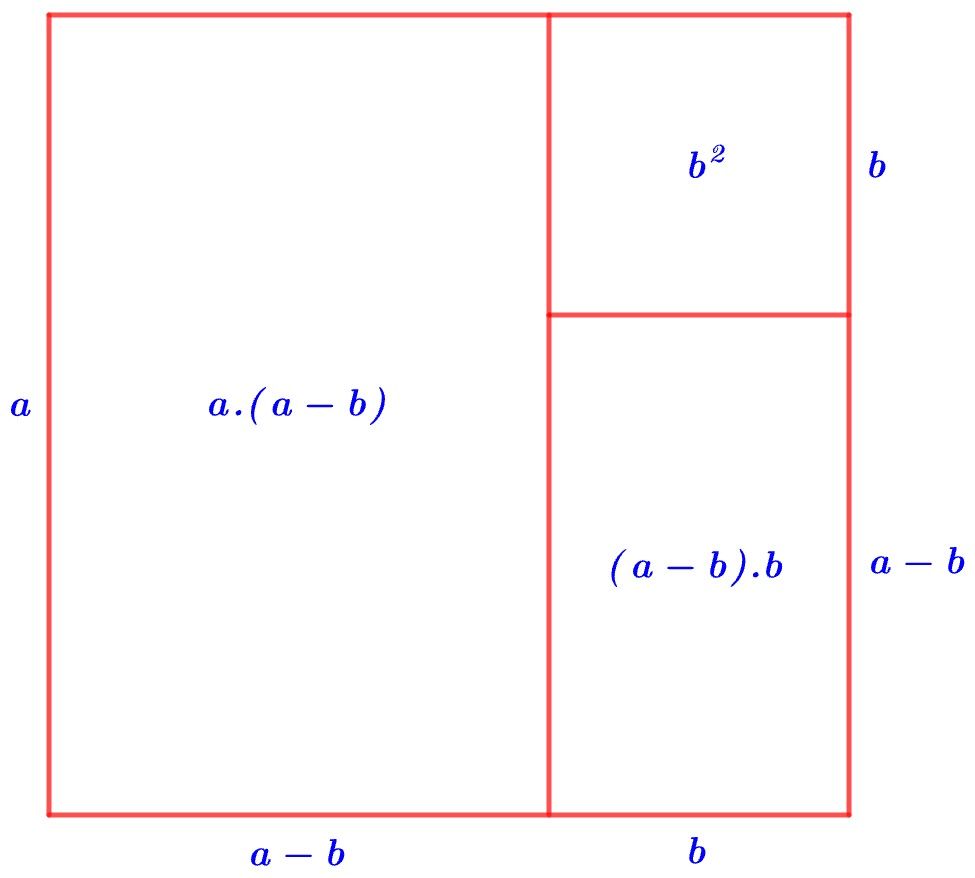
Geometrik şekil yardımıyla da yukarıdaki özdeşliğin ispatını yapabiliriz.

Yukarıdaki şekildeki büyük karenin alanı, küçük karenin alanı ile iki bir birine eş olmayan dikdörtgenin alanının toplamına eşittir. Buna göre;

$a^2=a.(a-b)+(a-b).b+b^2$

$a^2=a.(a-b)+b.(a-b)+b^2$

$a^2=(a-b).(a+b)+b^2$

$a^2-b^2=(a-b).(a+b)$ olur.