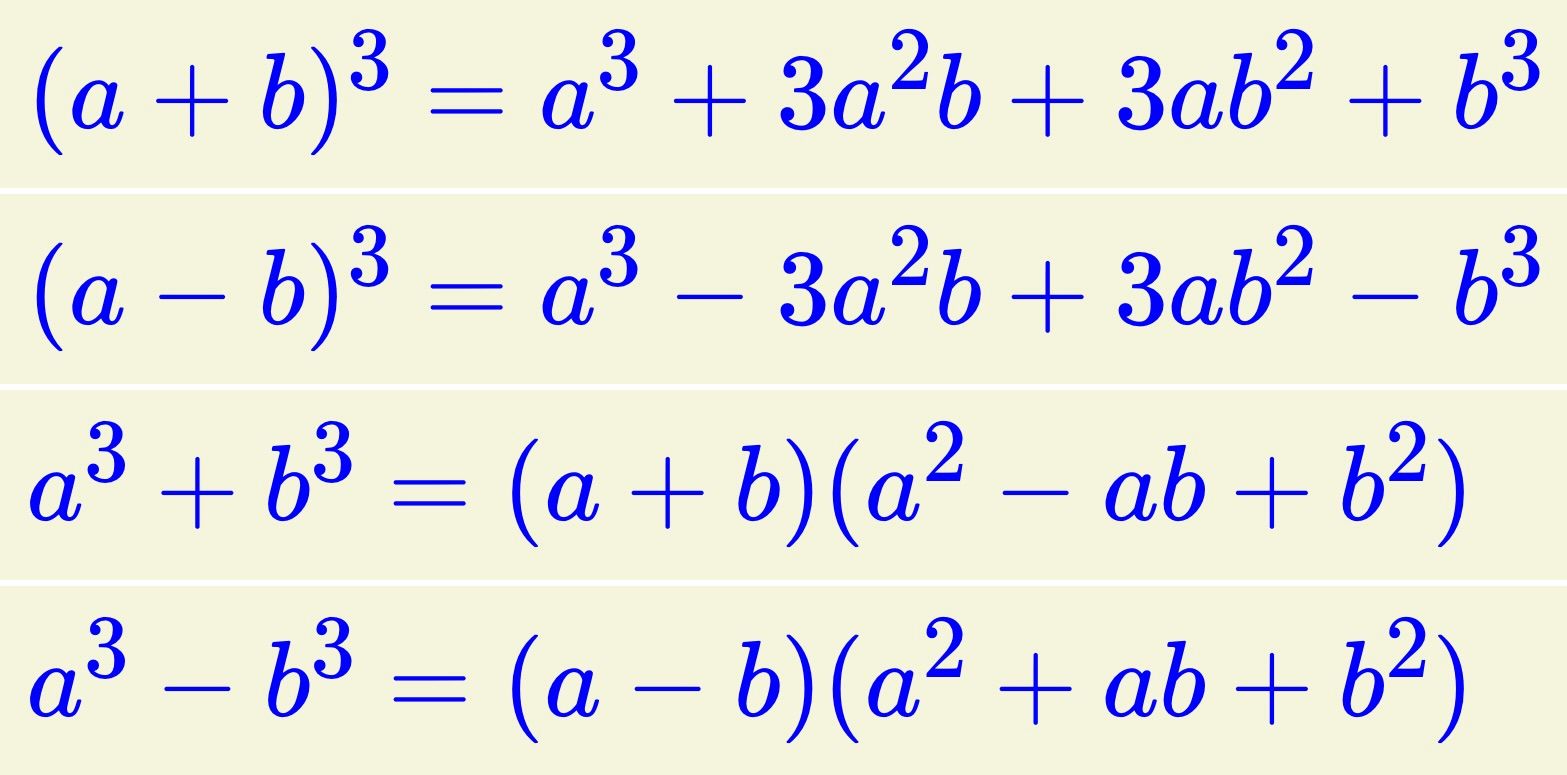Küp Açılımı

Küp Açılımı Formülleri

A. İki Cebirsel İfadenin Toplamının ve Farkının Küpü

1. İki Cebirsel İfadenin Toplamının Küpü

a + b şeklindeki bir cebirsel ifadenin küpü a³ + 3a²b + 3ab² + b³'e eşittir. Buna göre;

(a + b)³ = a³ + 3a²b + 3ab² + b³'tür. Bu ifadenin ispatını aşağıdaki şekildeki gibi gösterebiliriz.

İspatı

Çarpma işlemin toplama işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki özdeşliğin ispatını yapabiliriz.

$(a+b{)}^3=(a+b).(a+b).(a+b)$

İlk önce (a + b).(a + b)'nin değerini bulalım.

$(a+b).(a+b)=(a+b).a+(a+b).b$

$(a+b).(a+b)=a.(a+b)+b.(a+b)$

$(a+b).(a+b)=a.a+a.b+b.a+b.b$

$(a+b).(a+b)=a.a+a.b+a.b+b.b$

$(a+b).(a+b)=a^2+2.a.b+b^2$

Şimdi bulduğumuz bu değeri yukarıdaki eşitlikte yerine koyalım.

$(a+b{)}^3=(a^2+2.a.b+b^2).(a+b)$

$(a+b{)}^3=(a^2+2.a.b+b^2).a+(a^2+2.a.b+b^2).b$

$(a+b{)}^3=a.(a^2+2.a.b+b^2)+b.(a^2+2.a.b+b^2)$

$(a+b{)}^3=a.a^2+a.2.a.b+a.b^2+b.a^2+b.2.a.b+b.b^2$

$(a+b{)}^3=a^3+2.a^2.b+a.b^2+b.a^2+2.a.b^2+b^3$

$(a+b{)}^3=a^3+2.a^2.b+a.b^2+a^2.b+2.a.b^2+b^3$

$(a+b{)}^3=a^3+3.a^2.b+3.a.b^2+b^3$

2. İki Cebirsel İfadenin Farkının Küpü

a - b şeklindeki bir cebirsel ifadenin küpü a³ - 3a²b + 3ab² - b³'e eşittir. Buna göre;

(a - b)³ = a³ - 3a²b + 3ab² - b³'tür. Bu ifadenin ispatını aşağıdaki şekildeki gibi gösterebiliriz.

1. İspatı

Çarpma işlemin çıkarma işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki özdeşliğin ispatını yapabiliriz.

$(a-b{)}^3=(a-b).(a-b).(a-b)$

İlk önce (a - b).(a - b)'nin değerini bulalım.

$(a-b).(a-b)=(a-b).a-(a-b).b$

$(a-b).(a-b)=a.(a-b)-b.(a-b)$

$(a-b).(a-b)=a.a-a.b-b.a-b.-b$

$(a-b).(a-b)=a^2-a.b-b.a+b^2$

$(a-b).(a-b)=a^2-a.b-a.b+b^2$

$(a-b).(a-b)=a^2-2.a.b+b^2$

Şimdi bulduğumuz bu değeri yukarıdaki eşitlikte yerine koyalım.

$(a-b{)}^3=(a^2-2.a.b+b^2).(a-b)$

$(a-b{)}^3=(a^2-2.a.b+b^2).a-(a^2-2.a.b+b^2).b$

$(a-b{)}^3=a.(a^2-2.a.b+b^2)-b.(a^2-2.a.b+b^2)$

$(a-b{)}^3=a.a^2-a.2.a.b+a.b^2-b.a^2-b.-2.a.b-b.b^2$

$(a-b{)}^3=a^3-2.a^2.b+a.b^2-b.a^2+2.a.b^2-b^3$

$(a-b{)}^3=a^3-2.a^2.b+a.b^2-a^2.b+2.a.b^2-b^3$

$(a-b{)}^3=a^3-3.a^2.b+3.a.b^2-b^3$

2. İspatı

(a + b)³ = a³ + 3a²b + 3ab² + b³ özdeşliğinde, b gördüğümüz yere -b yazalım.

$[a+(-b){]}^3=a^3+3.a^2.(-b)+3.a.(-b{)}^2+(-b{)}^3$

$(a-b{)}^3=a^3+3.a^2.(-b)+3.a.b^2+(-b^3)$

$(a-b{)}^3=a^3-3.a^2.b+3.a.b^2-b^3$

B. İki Cebirsel İfadenin Küpünün Toplamı ve Farkı

1. İki Cebirsel İfadenin Küpünün Toplamı

a³ + b³ = (a + b).(a² - ab + b²)'dir.

1. İspatı

$a^3+3.a^2.b+3.a.b^2+b^3=(a+b{)}^3$

$a^3+b^3=(a+b{)}^3-3.a^2.b-3.a.b^2$

$a^3+b^3=(a+b{)}^3-3.a.b.(a+b)$

$a^3+b^3=(a+b{)}^2.(a+b)-3.a.b.(a+b)$

$a^3+b^3=(a^2+2.a.b+b^2).(a+b)-3.a.b.(a+b)$

$a^3+b^3=(a^2+2.a.b+b^2-3.a.b).(a+b)$

$a^3+b^3=(a^2-a.b+b^2).(a+b)$

$a^3+b^3=(a+b).(a^2-a.b+b^2)$

2. İspatı

Polinomlarda bölme işlemi kurallarından faydalanarak da ispatını yapabiliriz.

$\frac{a^3+b^3}{a+b}=a^2-ab+b^2$

$a^3+b^3=(a+b).(a^2-ab+b^2)$ olur.

2. İki Cebirsel İfadenin Küpünün Farkı

a³ - b³ = (a - b).(a² + ab + b²)'dir.

1. İspatı

$a^3-3.a^2.b+3.a.b^2-b^3=(a-b{)}^3$

$a^3-b^3=(a-b{)}^3+3.a^2.b-3.a.b^2$

$a^3-b^3=(a-b{)}^3+3.a.b.(a-b)$

$a^3-b^3=(a-b{)}^2.(a-b)+3.a.b.(a-b)$

$a^3-b^3=(a^2-2.a.b+b^2).(a-b)+3.a.b.(a-b)$

$a^3-b^3=(a^2-2.a.b+b^2+3.a.b).(a-b)$

$a^3-b^3=(a^2+a.b+b^2).(a-b)$

$a^3-b^3=(a-b).(a^2+a.b+b^2)$

2. İspatı

Polinomlarda bölme işlemi kurallarından faydalanarak da ispatını yapabiliriz.

$\frac{a^3-b^3}{a-b}=a^2+ab+b^2$

$a^3-b^3=(a-b).(a^2+ab+b^2)$ olur.