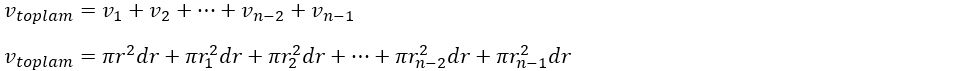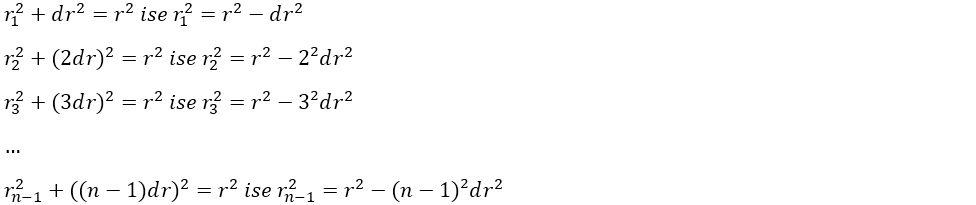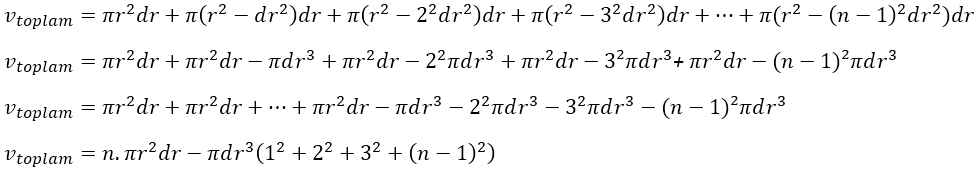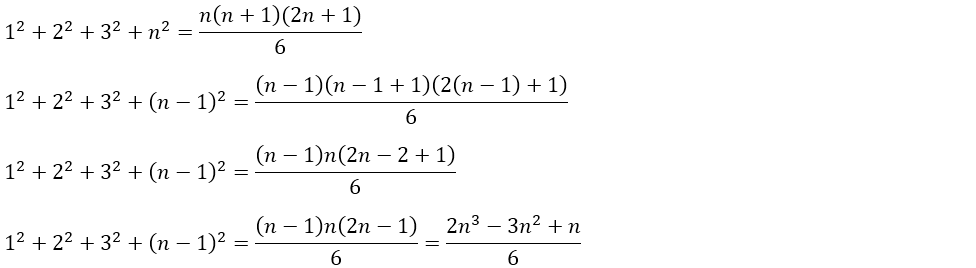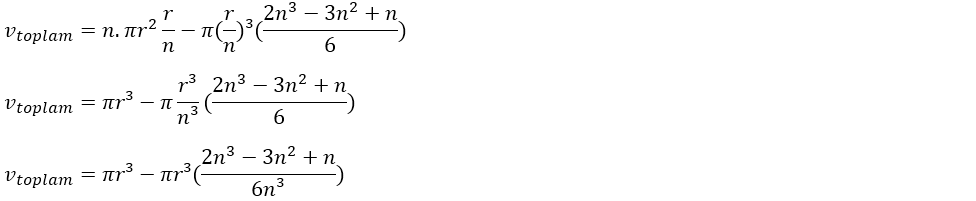Kürenin Hacmi

Küre Nedir ?

Üç boyutlu uzayda sabit bir noktadan eşit uzaklıktaki noktalar kümesinin oluşturduğu geometrik şekle küre denir. Sabit noktaya kürenin merkezi, kürenin merkezi ile yüzeyi üzerindeki herhangi bir nokta arasındaki uzaklığa ise kürenin yarı çapı denir. Küre, köşesi ve kenarı olmayan ilginç bir şekildir. Kendisi ile aynı yüzey alanına sahip geometrik şekiller arasında en büyük hacme sahiptir.

Kürenin Hacim Formülü

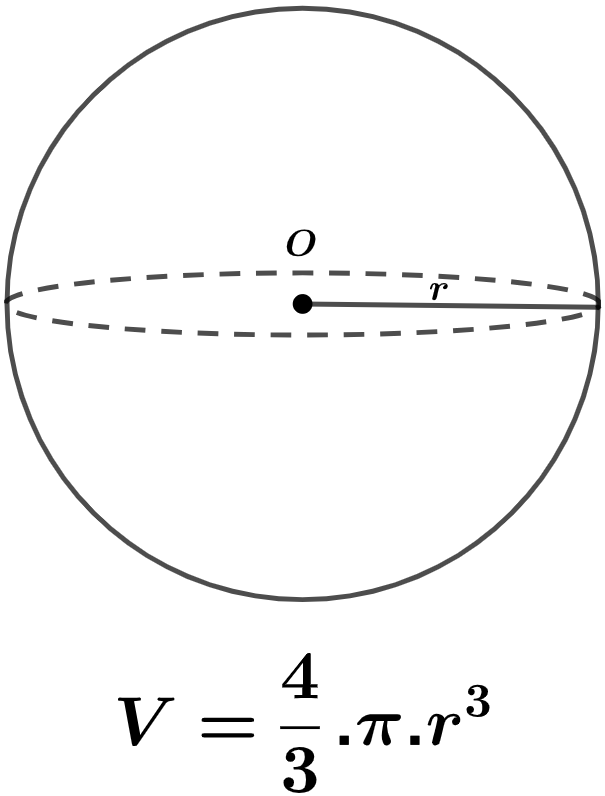
Yukarıdaki O merkezli, r yarıçaplı kürenin hacmi;

$V=\frac{4}{3}.\pi .r^3$

Eski Yunanlı matematikçi ve mühendis Arşimet (M.Ö. 287-212 ) kürenin hacmini hesaplayan ilk kişi olarak bilinmektedir.

Kürenin Hacmi Formülünün İspatı

Kürenin hacim formülü olan $\frac{4}{3}.\pi .r^3$'ün nereden geldiğini aşağıdaki şekildeki gibi ispatlayabiliriz.

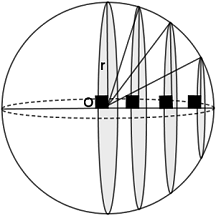
Bir kürenin hacmini doğrudan hesaplamak mümkün değildir. Bunun için onu hacmini kolayca hesaplayabileceğimiz silindir şeklinde parçalara ayırırız. Ancak ayırdığımız silindirlerin yükseklikleri bir birine eşit olmak zorundadır. Ayırdığımız silindirlerin sayısı arttıkça yükseklikleri de giderek küçülerek sonsuz küçüklükte bir değere ulaşır. Silindirlerin hacimlerinin toplamı kürenin hacmini verir.

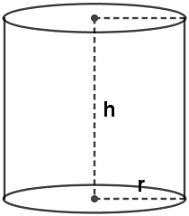
Yukarıdaki silindirin hacmi;

Hacim = Taban Alanı x Yükseklik

V = π.r².h

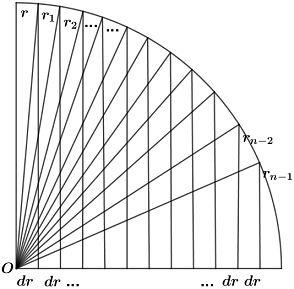
Küremizin yarıçapına r dersek, sonsuz incelikteki her bir silindir diliminin yüksekliği r/n olur. dr = r/n'dir. Buradaki "n" sonsuz büyüklükte bir değeri ifade eder iken "dr" ise sonsuz küçüklükte bir değeri ifade eder.

Yukarıdaki şekildeki r yarıçaplı silindirden başlamak üzere bütün silindirlerin hacimlerini sırasıyla toplayalım.

Örnek 1

Yarıçapının uzunluğu 6 cm olan bir kürenin hacmini bulunuz ? (π = 3,14)

V = 4.π.r³/3

V = 4.3,14.(6 cm)³/3

V = 4.3,14.216 cm³/3

V = 2712,96 cm³/3

V = 904,32 cm³

Örnek 2

Yarıçapları oranı 2 olan iki kürenin hacimleri oranı ne olur ?

1. kürenin yarıçapına r dersek, 2. kürenin yarıçapı 2r olur.

V1 = 4.π.r³/3

V2 = 4.π.(2r)³/3 = 4.π.8r³/3 = 32.π.r³/3

π.r³/3 = 1 olsun.

V1 = 4

V2 = 32 olur.

V1/V2 = 4/32

V1/V2 = 1/8

Kürenin Yüzey Alanı Formülü

Yarıçapının uzunluğu r olan bir kürenin yüzey alanının değeri;

Alan = 4.π.r²'dir.

Örnek 3

Yarıçapının uzunluğu 5 cm olan bir kürenin yüzey alanının değerini bulunuz ? (π = 3,14)

A = 4.π.r²

A = 4.3,14.(5 cm)²

A = 4.3,14.25 cm²

A = 314 cm²

Örnek 4

Yüzey alanının büyüklüğü 36π cm² olan bir kürenin hacminin değeri ne olur ?

4πr² = A

4πr² = 36π cm²

r² = 36π cm²/4π

r² = 9 cm²

√r² = √9 cm²

r = 3 cm

V = 4.π.r³/3

V = 4.π.(3 cm)³/3

V = 4.π.27 cm³/3

V = 108π cm³/3

V = 36π cm³