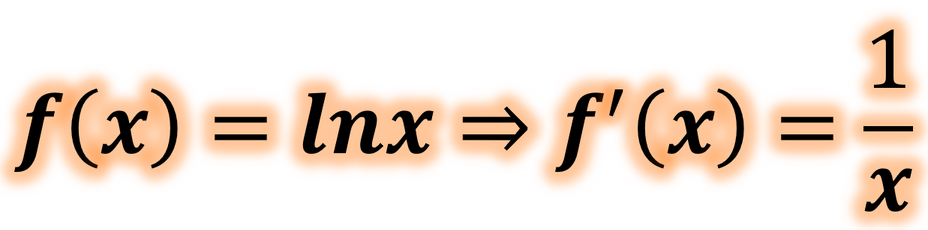lnx'in türevi

ln'in anlamı

Yeni Latince'de (Neo-Latince veya Modern Latince), "doğal logaritma" anlamına gelen logarithmus naturalis sözcüklerinin ilk harflerinden (l ve n) türetilmiştir. İnsanlar tarafından sonradan üretilen 2'lik, 5'lik, 10'luk veya 60'lık gibi bir sayı tabanı olmayıp kendiliğinden (doğal olarak) ortaya çıkan bir sayı tabanı olduğu için kendisine bu isim verilmiştir.

e tabanına göre, 0'dan büyük bir x sayısının logaritması (üssü), lnx'e eşittir. Buradaki e, π gibi irrasyonel bir sayı olup, ilk birkaç basamağı 2,718281... şeklindedir.

$e^{lnx}=x(x>0)$

$ln{e}^x=x$

Örneğin, e (2,718281...) tabanına göre, 5 sayısının logaritması veya üssü ln5'e eşittir. ln5'in sonucunun kaça eşit olduğunu bulmak istersek çok fonksiyonlu bir hesap makinesinde önce ln tuşuna sonra da 5'e basarak 1,6094... sonucunu bulabiliriz.

e için yazılabilecek birkaç önemli eşitlik aşağıda gösterilmiştir.

$e=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+...$

$e=\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n$

$e=\underset{h\to 0}{\lim }(1+h{)}^{\frac{1}{h}}$

lnx'in türevi nedir ?

$f(x)=lnx\Rightarrow f^{\prime }(x)=\frac{1}{x}(x>0)$ olur.

lnx'in türevinin ispatı

Lnx türevinin neden 1/x'e eşit olduğunu türevin ikinci tanımından yola çıkarak aşağıdaki şekildeki gibi ispatlayabiliriz.

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

$(lnx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{ln(x+h)-lnx}{h}$

$(lnx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{ln(\frac{x+h}{x})}{h}$

$(lnx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{ln(\frac{\cancel{x}}{\cancel{x}}+\frac{h}{x})}{h}$

$(lnx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{ln(1+\frac{h}{x})}{h}$

Yukarıdaki eşitlikte hem payı hem de paydayı $\frac{x}{h}$ ile çarpalım.

$(lnx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{ln(1+\frac{h}{x}).\frac{x}{h}}{\cancel{h}.\frac{x}{\cancel{h}}}$

$(lnx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{\frac{x}{h}.ln(1+\frac{h}{x})}{x}$

$(lnx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{ln(1+\frac{h}{x}{)}^{\frac{x}{h}}}{x}$

Yukarıdaki eşitlikte $\frac{x}{h}=n$ dönüşümü yapılırsa;

$\frac{h}{x}=\frac{1}{n}$ olur.

$\frac{x}{h}=n$ eşitliğinde;

$h$ değeri sıfıra doğru $(h\to 0)$ giderken, $n$ değeri sonsuza doğru $(n\to \infty )$ gider.

$(lnx{)}^{\prime }=\underset{n\to \infty }{\lim }\frac{ln(1+\frac{1}{n}{)}^n}{x}$

$(lnx{)}^{\prime }=\underset{n\to \infty }{\lim }\frac{1}{x}.ln(1+\frac{1}{n}{)}^n$

$(lnx{)}^{\prime }=\frac{1}{x}.\underset{n\to \infty }{\lim }ln(1+\frac{1}{n}{)}^n$

$(lnx{)}^{\prime }=\frac{1}{x}.ln[\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n]$

$\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n=e$

$(lnx{)}^{\prime }=\frac{1}{x}.lne$

$(lnx{)}^{\prime }=\frac{1}{x}.1$

$(lnx{)}^{\prime }=\frac{1}{x}$

Ln fonksiyonu karmaşık gibi görünen çok sayıdaki fonksiyonun türevinin alınmasında oldukça kullanışlıdır. Örneğin, $f(x)=g(x).h(x)$ şeklindeki bir fonksiyonun türevi (çarpımın türevi), $f^{\prime }(x)=g^{\prime }(x).h(x)+h^{\prime }(x).g(x)$'dir.

Ln fonksiyonunu kullanarak bu eşitliği aşağıdaki şekildeki gibi ispatlayabiliriz.

$f(x)=g(x).h(x)$

$lnf(x)=ln[g(x).h(x)]$

$lnf(x)=lng(x)+lnh(x)$

$[lnf(x){]}^{\prime }=[lng(x)+lnh(x){]}^{\prime }$

$[lnf(x){]}^{\prime }=[lng(x){]}^{\prime }+[lnh(x){]}^{\prime }$

$\frac{f^{\prime }(x)}{f(x)}=\frac{g^{\prime }(x)}{g(x)}+\frac{h^{\prime }(x)}{h(x)}$

$\frac{f^{\prime }(x)}{f(x)}=\frac{g^{\prime }(x).h(x)+h^{\prime }(x).g(x)}{g(x).h(x)}$

$\frac{f^{\prime }(x)}{\cancel{f(x)}}=\frac{g^{\prime }(x).h(x)+h^{\prime }(x).g(x)}{\cancel{f(x)}}$

$f^{\prime }(x)=g^{\prime }(x).h(x)+h^{\prime }(x).g(x)$