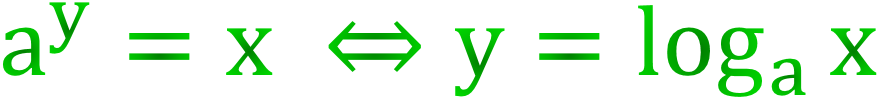Logaritma Nedir ?
Logaritma sözcüğü, Eski Yunanca'da "oran" anlamına gelen λόγος (lógos) ile "sayı" anlamına gelen αριθμός (arithmós) sözcüklerinden türetilmiştir.
Örneğin 625 sayısını, 5x5x5x5 veya 5⁴ şeklinde de yazabiliriz. 5'in üzerindeki 4 sayısı, 5'in yan yana kaç kere kendi kendisiyle çarpılacağını gösterir. Burada 5'e taban, 4 ise üs veya kuvvet denir. 5⁴ ifadesi, "5 üzeri 4" veya "5 üssü 4" şeklinde okunur.
Üslü sayılarda üs veya kuvvete, logaritma da denir. Logaritma genelde log şeklinde ifade edilir. 5⁴ = 625 ise 625'in 5 tabanına göre logaritması 4'tür. log₅ 625 = 4 İfadesi, "5 tabanına göre 625'in logaritması 4'tür" şeklinde okunur. Logaritma bir üs (kuvvet) bulma işlemidir.
2⁷ = 128 ⇔ log₂ 128 = 7
6³ = 216 ⇔ log₆ 216 = 3
10⁵ = 10000 ⇔ log₁₀ 10000 = 5
5⁰ = 1 ⇔ log₅ 1 = 0
9⁰∙⁵ = 3 ⇔ log₉ 3 = 0.5 = 1/2
16⁰∙²⁵ = 2 ⇔ log₁₆ 2 = 0.25 = 1/4
Logaritmanın değeri sıfır veya sıfırdan büyük kesirli bir sayı olabileceği gibi sıfırdan küçük bir sayı da olabilir.
2⁸ (256) Sayısının karekökü 2⁴ (16) sayısına eşittir. Buradan, bir sayının karekökünü bulmak istediğimizde logaritmasını ikiye bölmemiz gerektiğini anlarız. Çünkü 256 sayısının 2 tabanına göre logaritması olan 8'i ikiye bölersek, 16 sayısının 2 tabanına göre logaritması olan 4'ü elde ederiz. 5⁶ (15625) sayısının küpkökü 5² (25) sayısına eşittir. Buradan, bir sayının küpkökünü bulmak istediğimizde logaritmasını üçe bölmemiz gerektiğini anlarız. Çünkü 15625 sayısının 5 tabanına göre logaritması olan 6'yı üçe bölersek, 25 sayısının 5 tabanına göre logaritması olan 2'yi elde ederiz.
Logaritma Fonksiyonunun Tanımı
a ϵ R⁺ ve a ≠ 1 olmak üzere, f: R → R⁺, y = f(x) = xᵃ üstel fonksiyonunun tersi olan f⁻¹: R⁺ → R , y = f(x) = logₐ x fonksiyonuna logaritma fonksiyonu denir.
Bayağı Logaritma ve Doğal Logaritma
Tabanın 10 olduğu logaritmaya, bayağı logaritma denir. Bayağı logaritma fonksiyonu y = f(x) = log₁₀ x yerine daha çok y = f(x) = log x şeklinde gösterilir. Tabanın e (2.7182818284...) olduğu logaritmaya ise doğal logaritma denir. Doğal logaritma fonksiyonu ise y = f(x) = logₑ x yerine daha çok y = f(x) = ln x şeklinde gösterilir.
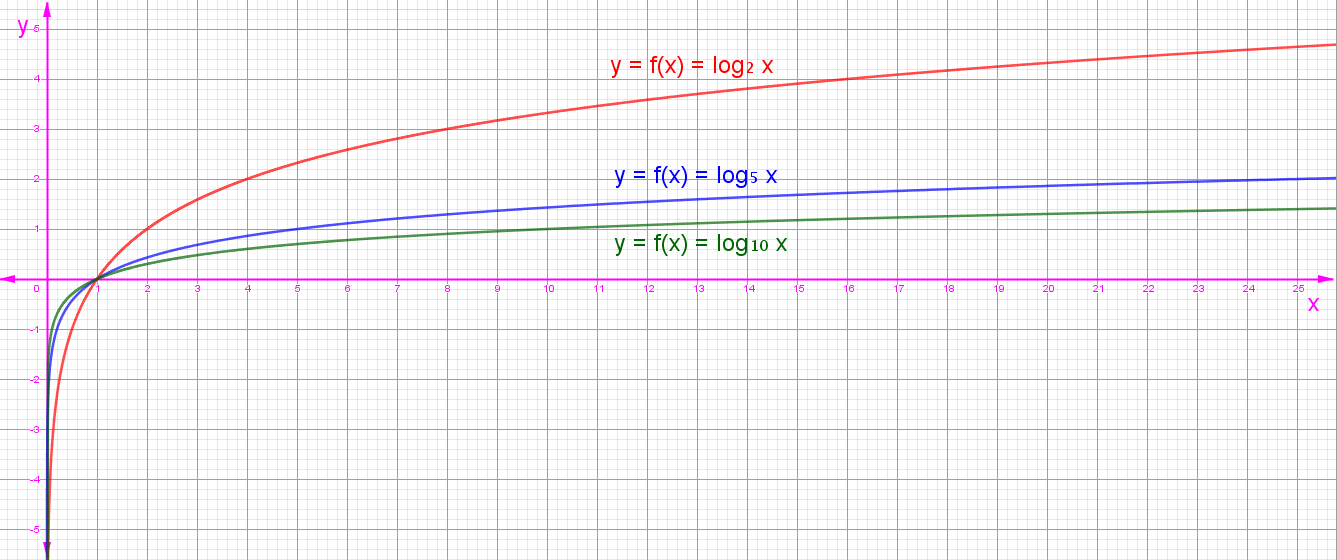
Logaritma Fonksiyonunun Grafiği
Logaritma Fonksiyonunun Özellikleri
1. Her tabana göre 1'in logaritması 0'dır.
a ϵ R⁺ ve a ≠ 1 olmak üzere; logₐ 1 = 0
logₐ 1 = m olsun.
aᵐ = 1 olur.
a⁰ = k olsun. (x, k ≠ 0)
a⁰/k = k/k
a⁰/a⁰ = 1
a⁰⁻⁰ = 1
a⁰ = 1
aᵐ = a⁰
m = 0 olur.
Örnek: log₂ 1 = 0, log₅ 1 = 0, log 1 = 0, ln 1 = 0
2. 1'den farklı her pozitif tam sayının kendi tabanına göre logaritması 1'e eşittir.
a ϵ R⁺ ve a ≠ 1 olmak üzere; logₐ a = 1
logₐ a = m olsun.
aᵐ = a olur.
aᵐ = a¹
m = 1 olur.
Örnek: log₃ 3 = 1, log₉ 9 = 1, log 10 = 1, ln e = 1
3. Tabanları aynı iki sayının çarpımının logaritması, sayıların ayrı ayrı logaritmalarının toplamına eşittir. Aynı ifadeyi tersten söylersek tabanları aynı iki sayının logaritmalarının toplamı, sayıların çarpımının logaritmasına eşittir.
a, x ve y ϵ R⁺ ve a ≠ 0 olmak üzere; logₐ (x.y) = logₐ x + logₐ y
logₐ x = m ve logₐ y = n olsun.
aᵐ = x ve aⁿ = y olur.
x.y = aᵐ.aⁿ
x.y = aᵐ⁺ⁿ
x.y = aᵗ olsun.
logₐ (x.y) = t olur.
aᵗ = aᵐ⁺ⁿ
t = m + n
logₐ (x.y) = logₐ x + logₐ y olur.
Örnek: log₂ (8.32) = ?
log₂ (8.32) = log₂ 8 + log₂ 32
log₂ (8.32) = 3 + 5
log₂ (8.32) = 8
4. Tabanları aynı iki sayının bölümünün logaritması, sayıların ayrı ayrı logaritmalarının farkına eşittir. Aynı ifadeyi tersten söylersek tabanları aynı iki sayının logaritmalarının farkı, sayıların bölümünün logaritmasına eşittir.
a, x ve y ϵ R⁺ ve a, y ≠ 0 olmak üzere; logₐ (x/y) = logₐ x - logₐ y
logₐ x = m ve logₐ y = n olsun.
aᵐ = x ve aⁿ = y olur.
x/y = aᵐ/aⁿ
x/y = aᵐ⁻ⁿ
x/y = aᵗ olsun.
logₐ (x/y) = t olur.
aᵗ = aᵐ⁻ⁿ
t = m - n
logₐ (x/y) = logₐ x - logₐ y olur.
Örnek: log₃ (243/27) = ?
log₃ (243/27) = log₃ 243 - log₃ 27
log₃ (243/27) = 5 - 3
log₃ (243/27) = 2
5. Üslü bir ifadenin logaritması alınırken üs dışarı çıkarılarak da logaritma alınabilir.
a ve b ϵ R⁺, m ϵ R olmak üzere; logₐ bᵐ = m.logₐ b
bᵐ = b.b.b...b (m tane b)
logₐ bᵐ = logₐ (b.b.b...b)
logₐ (x.y) = logₐ x + logₐ y
logₐ bᵐ = logₐ b + logₐ b + logₐ b + . . . + logₐ b (m tane logₐ b)
logₐ bᵐ = m.logₐ b
Örnek: log₆ 3⁵ = 5.log₆ 3, log₅ ∛9 = 1/3.log₅ 9, Log₄ 5⁻⁶ = -6.Log₄ 5
6. Tabanı üslü bir ifadenin logaritması alınırken üs çarpma işlemine göre ters çevrilip dışarı alınarak da logaritma alınabilir.
a ve b ϵ R⁺, n ϵ R ve n ≠ 0 olmak üzere; logₐⁿ b = 1/n.logₐ b
logₐⁿ b = m olsun.
(aⁿ)ᵐ = b olur.
aⁿᵐ = b
aᵐ = b¹˸ⁿ
logₐ b¹˸ⁿ = m
logₐ bᵐ = m.logₐ b
1/n.logₐ b = m
1/n.logₐ b = logₐⁿ b
Örnek: log₅³ 100 = 1/3.log₅ 100, log₂⁵ 30 = 1/5.log₂ 30, log₁₀⁻⁴ 25 = -1/4.log₁₀ 25
7. Yukarıdaki iki formülü birleştirirsek;
logₐⁿ bᵐ = m.logₐⁿ b
logₐⁿ bᵐ = m.1/n.logₐ b
logₐⁿ bᵐ = m/n.logₐ b olur.
Örnek: Log₅⁴ 2⁷ = 7/4.Log₅ 2, log₃² 5³ = 3/2.log₃ 5, Log₄⁵ 10² = 2/5.Log₄ 10
8. Taban ile sayı yer değiştirirse çarpma işlemine göre önceki logaritmanın tersi elde edilir.
a ve x ϵ R⁺ olmak üzere; logₓ a = 1/logₐ x
logₐ x = y olsun.
aʸ = x olur.
logₓ a = logₐʸ a
logₓ a = 1/y.logₐ a
logₓ a = 1/y.1
logₓ a = 1/y
logₓ a = 1/logₐ x
Örnek: log₂ 5 = 1/log₅ 2, log₁₀ 7 = 1/log₇ 10, log₉ 3 = 1/log₃ 9
9. Logaritmada taban değişikliği;
a, b ve x ϵ R⁺ olmak üzere; logₐ b = logₓ b/logₓ a
logₓ b = m ve logₓ a = n olsun.
xᵐ = b ve xⁿ = a olur.
logₐ b = logₓⁿ xᵐ
logₐ b = m/n.logₓ x
logₐ b = m/n.1
logₐ b = m/n
logₐ b = logₓ b/logₓ a
Örnek: log₃ 8 = ?
Ortak tabanı 10 seçelim.
log₃ 8 = log₁₀ 8/log₁₀ 3
log₃ 8 = log 8/log 3
