Mutlak Değer

Mutlak Değer Nedir?

Mutlak değer kısaca sayı doğrusu üzerinde yer alan herhangi bir noktanın sıfır noktasına olan uzaklığı olarak tanımlanabilir. Mutlak değer "| |" şeklinde gösterilir. Uzaklık hiçbir zaman eksi (-) olamayacağı için mutlak değer her zaman için (sıfır dışında) pozitif (+) yani sıfırdan büyüktür.

Mutlak Değer Fonksiyonunun Tanımı

x ∈ R ve |x| mutlak değer fonksiyonu olmak üzere;

Yukarıdaki mutlak değer fonksiyonunun tanımından da anlaşılacağı üzere mutlak değer hiç bir zaman sıfırdan küçük (negatif) olamaz, ancak sıfır veya sıfırdan büyük olabilir.

Mutlak Değerle İlgili Önemli Kural

1. Mutlak değerin içindeki sayının işareti eğer pozitif ise bu sayı mutlak değerin dışına çıkarken işaret değiştirmeden aynen çıkar.

Örnek

|+ 5| = 5

|3/2| = 3/2

|+ 8| = 8

2. Mutlak değerin içindeki sayı eğer sıfır ise mutlak değerin değeri de sıfır olur.

Örnek

|0| = 0

3. Mutlak değerin içindeki sayının işareti eğer negatif ise bu sayı mutlak değerin dışına çıkarken işaret değiştirerek veya önüne - işareti alarak çıkar.

Örnek

|- 7| = - ( - 7) = 7

|- 4/9| = - (- 4/9) = 4/9

|- 3| = - (- 3) = 3

Örnek 1

2 < x < 3 olmak üzere |x - 5| + |x + 3| ifadesinin en sade şekli nedir?

Cevap

2 < x < 3

2 - 5 < x - 5 < 3 - 5

- 3 < x - 5 < - 2 olur ve sonuç olarak x - 5 sıfırdan küçük olacağı için mutlak değer dışına çıkarken önüne - işareti alarak çıkar.

2 < x < 3

2 + 3 < x + 3 < 3 + 3

5 < x + 3 < 6 olur ve sonuç olarak x + 3 sıfırdan büyük olacağı için mutlak değerin dışına çıkarken işaret değiştirmeden aynen çıkar.

|x - 5| + |x + 3| = - (x - 5) + (x + 3)

|x - 5| + |x + 3| = - x + 5 + x + 3

|x - 5| + |x + 3| = 8 olur.

Örnek 2

x < 0 < y olmak üzere |x - y| + |y - x| ifadesinin en sade şekli nedir?

Cevap

x < 0

0 < y

x + 0 < y + 0

x < y olur.

x < y ⇒ x - y < 0 olur.

x - y < 0 ⇒ y - x > 0 olur.

|x - y| + |y - x| = - (x - y) + (y - x)

|x - y| + |y - x| = - x + y + y - x

|x - y| + |y - x| = 2y - 2x olur.

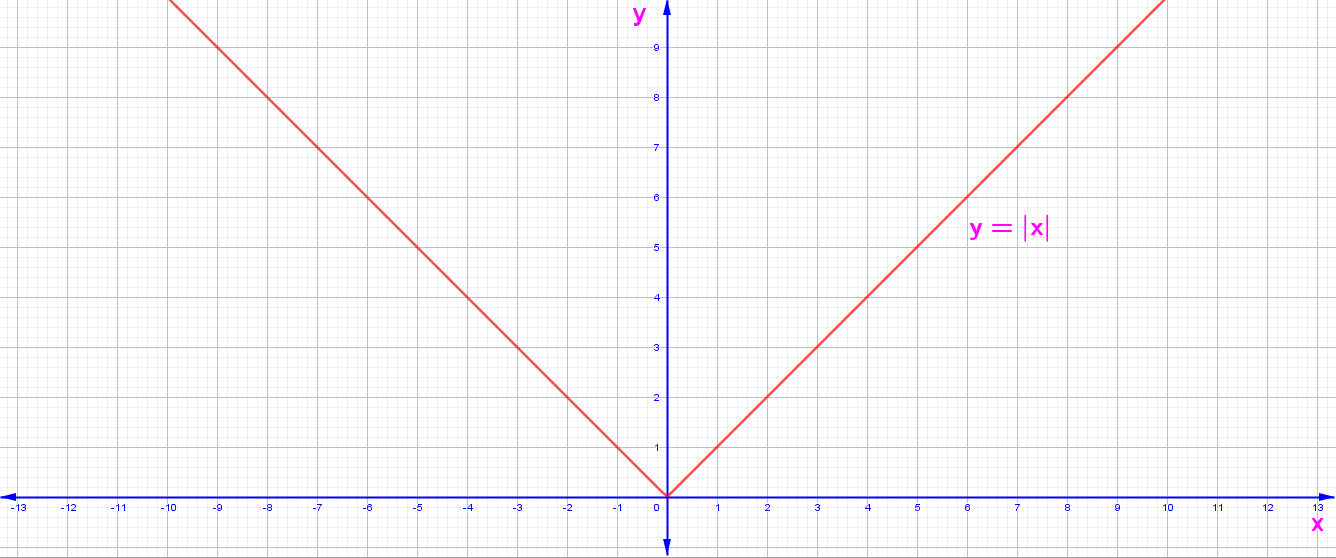
Mutlak Değer Fonksiyonunun Grafiği

Mutlak Değer Özellikleri

x, y ∈ R olmak üzere;

1. |x| ≥ 0

Bir reel (gerçel) sayının mutlak değeri her zaman için 0'a eşit veya 0'dan büyüktür.

2. |x| = |- x|

Bir reel (gerçel) sayının toplama işlemine göre tersinin mutlak değeri ile sayının kendisinin mutlak değeri bir birine eşittir.

3. |x . y . z| = |x| . |y| . |z|

Çarpım durumundaki reel (gerçel) sayıların mutlak değeri bu sayıların ayrı ayrı mutlak değerlerinin çarpımına eşittir.

4. y ≠ 0 olmak üzere; |x / y| = |x| / |y|

Bölüm durumundaki iki reel (gerçel) sayının mutlak değeri bu sayıların ayrı ayrı mutlak değerlerinin bölümüne eşittir.

5. a ∈ Z olmak üzere; |xª| = |x|ª

Bir reel (gerçel) sayının tam sayı kuvvetinin mutlak değeri mutlak değerinin aynı kuvvetine eşittir.

6. |x + y| ≤ |x| + |y|

İki reel (gerçel) sayının toplamının mutlak değeri sayıların ayrı ayrı mutlak değerlerinin toplamından küçük veya eşittir. Sayılardan biri negatif biri pozitif ise küçük, ikisinin işareti de aynı ise eşittir.

7. |x - y| ≥ |x| - |y|

İki reel (gerçel) sayının farkının mutlak değeri sayıların ayrı ayrı mutlak değerlerinin farkından büyük veya eşittir. Sayılardan biri negatif biri pozitif ise büyük, ikisinin işareti de aynı ise eşittir.

8. √x² = |x|

Kareköklü bir ifade de kök içindeki reel (gerçel) sayı kök dışına çıkarken mutlak değer şeklinde çıkar.

9. ||x|| = |x|

Bir reel (gerçel) sayının mutlak değerin mutlak değeri, mutlak değerdir.

Mutlak Değerli Denklemler

Mutlak değerden oluşan denklemlere mutlak değerli denklem denir.

Mutlak Değerli Denklemlerin Çözümü

1. |x| = a Şeklindeki Denklemler

a. x > 0 ise x = a olur.

b. x = 0 ise 0 = a olur.

c. x < 0 ise - x = a olur.

Not: a < 0 olursa denklemin çözümü yoktur ve çözüm kümesi de boş kümedir.

Örnek 1

|x + 3| = 5 ise denkleminin çözüm kümesi nedir?

Cevap

x + 3 > 0 ise;

x + 3 = 5

x = 5 - 3

x = 2 olur.

x + 3 < 0 ise;

- (x + 3) = 5

- x - 3 = 5

- x = 5 + 3

- x = 8

x = - 8 olur.

Ç. K. = {- 8, 2}

Örnek 2

|2x - 5| = 4 - x denkleminin çözüm kümesi nedir?

Cevap

2x - 5 > 0 ise;

2x - 5 = 4 - x

2x + x = 4 + 5

3x = 9

x = 3 olur.

2x - 5 < 0 ise;

- (2x - 5) = 4 - x

- 2x + 5 = 4 - x

- 2x + x = 4 - 5

- x = - 1

x = 1 olur.

sağlamasını yapalım.

x = 3 için;

|2x - 5| = 4 - x

|2 . 3 - 5| = 4 - 3

|6 - 5| = 1

|1| = 1

1 = 1

x = 1 için;

|2x - 5| = 4 - x

|2 . 1 - 5| = 4 - 1

|2 - 5| = 3

|- 3| = 3

3 = 3

Ç. K. = {1, 3}

2. |x| = |a| Şeklindeki Denklemler

a. x = a

b. x = - a

Örnek 1

|2x - 3| = |5| denkleminin çözüm kümesi nedir?

Cevap

2x - 3 = 5

2x = 5 + 3

2x = 8

x = 4 olur.

2x - 3 = - 5

2x = - 5 + 3

2x = - 2

x = - 1 olur.

Ç. K. = {- 1, 4}

Örnek 2

|x + 2| = |5 - 2x| denkleminin çözüm kümesi nedir?

Cevap

x + 2 = 5 - 2x

x + 2x = 5 - 2

3x = 3

x = 1 olur.

x + 2 = - (5 - 2x)

x + 2 = - 5 + 2x

x - 2x = - 5 - 2

- x = - 7

x = 7 olur.

Ç. K. = {1, 7}

Mutlak Değerli Eşitsizlikler

Mutlak değerden oluşan eşitsizliklere mutlak değerli eşitsizlik denir.

Mutlak Değerli Eşitsizliklerin Çözümü

1. |x| ≤ a Şeklindeki Eşitsizliklerin Çözümü

a. a > 0 ise - a ≤ x ≤ a olur.

b. a = 0 ise x = 0 olur.

c. a < 0 ise Ç. K. = { }

Örnek 1

|x - 3| < 5 eşitsizliğinin çözüm aralığı nedir?

Cevap

- 5 < x - 3 < 5

- 5 + 3 < x - 3 + 3 < 5 + 3

- 2 < x < 8

Ç. K. = [- 2, 8]

2. |x| ≥ a Şeklindeki Eşitsizliklerin Çözümü

a. a > 0 ise x ≥ a ve x ≤ - a olur.

b. a = 0 ise Ç. K. = {R}

c. a < 0 ise Ç. K. = {R }

Örnek 1

|2x + 4| ≥ 6 eşitsizliğinin çözüm aralığı nedir?

Cevap

2x + 4 ≥ 6

2x ≥ 6 - 4

2x ≥ 2

x ≥ 1

2x + 4 ≤ - 6

2x ≤ - 6 - 4

2x ≤ - 10

x ≤ - 5

Ç. K. = (− ∞, - 5] U [1, + ∞)

3. a ≤ |x| ≤ b Şeklindeki Eşitsizliklerin Çözümü

a > 0 ve b > 0 ise eşitsizliğinin çözümü

a ≤ x ≤ b veya - b ≤ x ≤ - a şeklinde olur.

Örnek 1

3 < |2x + 1| ≤ 5 eşitsizliğinin çözüm kümesi nedir?

Cevap

3 < 2x + 1 ≤ 5

3 - 1 < 2x + 1 - 1 ≤ 5 - 1

2 < 2x ≤ 4

1 < x ≤ 2

- 5 ≤ 2x + 1 < - 3

- 5 - 1 ≤ 2x + 1 - 1 < - 3 - 1

- 6 ≤ 2x - 4

- 3 ≤ x - 2

Ç. K. = [- 3, - 2) U (1, 2]