Öklid Teoremi (Öklid Bağıntısı)

Pow
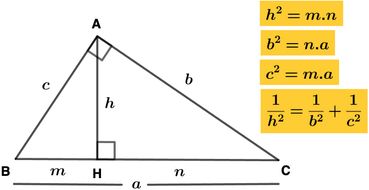
Bir dik üçgendeki dik kenarlar, hipotenüs ve hipotenüse ait yükseklik arasındaki bağlantıyı açıklamaya çalışan teoreme "Öklit Teoremi" denir.
Öklit Teoremi (Öklit Bağıntısı)
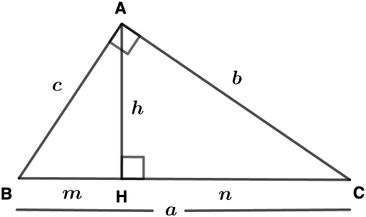
Bir dik üçgende dik açının bulunduğu köşeden hipotenüse bir dikme inilirse iki yeni dik üçgen oluşur. Oluşan bu iki yeni dik üçgen ile ilk dik üçgen Açı-Açı-Açı (A. A. A.) bakımından benzer üçgenlerdir. İşte bu üçgenlerden yararlanarak elde edilen bağıntılara "Öklit Bağıntısı" denir.
1. Öklid'in Yükseklik Bağıntısı
İspat
2. Öklid'in Dik Kenar Bağıntıları
1.
İspatı
2.
İspat
3.
İspat
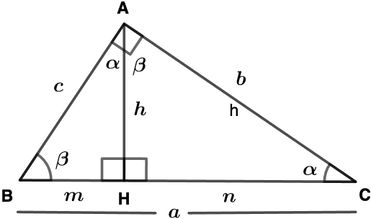
Üçgenlerdeki Benzerlik Kurallarından Yararlanarak Öklid Bağıntılarının İspatı
Yukarıdaki şekildeki ABC, HBA ve HAC dik üçgenleri Açı-Açı-Açı (A. A. A.) bakımından benzer üçgenlerdir.
1. Eşitliğinin İspatı
2. Eşitliğinin İspatı
3. Eşitliğinin İspatı
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.