Pi Sayısının (π-=-3,141592654…) Değerini Nasıl Bulabiliriz

Pow
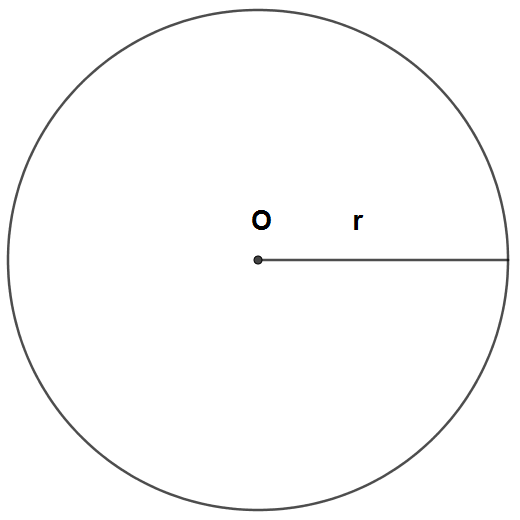
Çember geometride, sabit bir noktadan eşit uzaklıktaki noktalar kümesi (topluluğu) olarak tanımlanır. Çizdiğimiz herhangi bir çemberin çevresinin çapına oranı p
Çember geometride, sabit bir noktadan eşit uzaklıktaki noktalar kümesi (topluluğu) olarak tanımlanır. Çizdiğimiz herhangi bir çemberin çevresinin çapına oranı pi (π) dediğimiz sabit bir sayıya eşittir. Pi sayısının ilk birkaç basamağı 3,141592654... şeklindedir. O zaman aklımıza şu soru gelebilir neden bütün çemberlerin çevresinin çapına oranı sabit bir sayı olan pi sayısına (π = 3,141592654…) eşittir.
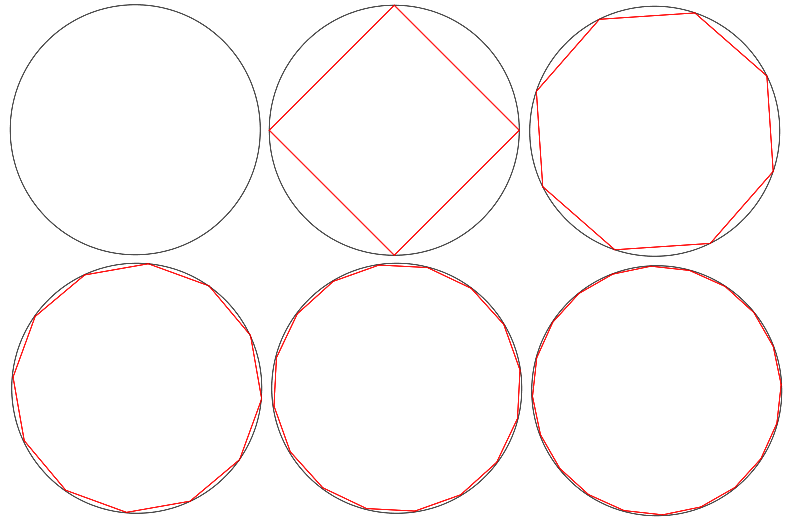
Aşağıdaki şekillere dikkatlice bakarsak bir çemberin içerisine çizilen düzgün çokgenlerin kenar sayısı artıkça bu çokgenlerin giderek bir çembere benzemeye başladığı görülür. Son çemberin içerisine çizeceğimiz son düzgün çokgeninin kenar sayısı sonsuza ulaşacağı için bu düzgün çokgen artık bir çember olarak görünecektir.
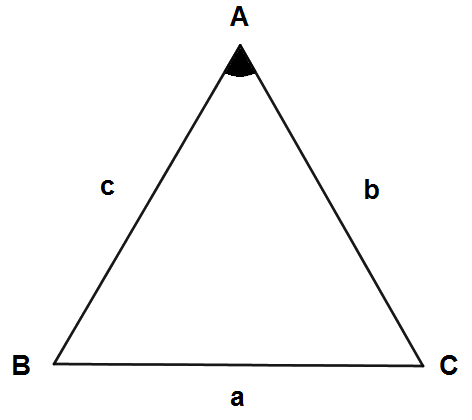
Kosinüs Teoremine göre iki kenarı ve bir açısı bilinen bir üçgenin üçüncü kenarını aşağıdaki şekilde hesaplayabiliriz.
a² = b² + c² - 2.b.c.cosA
√a² = √b² + c² - 2.b.c.cosA
a = √b² + c² - 2.b.c.cosA değerine eşittir.
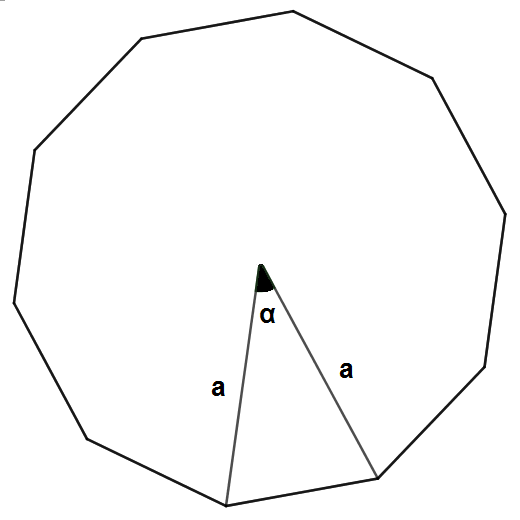
Yukarıdaki Formülden yola çıkarak n kenarlı bir düzgün çokgenin çevresini aşağıdaki şekilde hesaplayabiliriz.
Çevre = n.√a² + a² - 2.a.a.cosα
Çevre = n.√2.a² - 2.a².cosα
Çevre = n.√2.a².(1 - cosα)
Çevre = n.√2.a.√1 - cosα olur.
Çevresini hesapladığımız düzgün çokgenlerden elde ettiğimiz sonuçları 2a'ya bölelim. Bir çemberin yarıçapına r dersek buradaki a, r değerine eşit olur.
Dörtgen = 4.√2.a.√(1 – cos360/4) = 5,656854249.a ise 5,656854249.a/2.a = 2,8284271245
Sekizgen = 8.√2.a.√(1 – cos360/8) = 6,122934918.a ise 6,122934918.a/2.a = 3,061467459
Onikigen = 12.√2.a.√(1 – cos360/12) = 6,211657082.a ise 6,211657082.a/2.a = 3,105828541
Onaltıgen = 16.√2.a.√(1 – cos360/16) = 6,242890305.a ise 6,242890305.a/2.a = 3,1214451525
Yirmigen = 20.√2.a.√(1 – cos360/20) = 6,257378602.a ise 6,257378602.a/2.a = 3,128689301
Elligen = 50.√2.a.√(1 – cos360/50) = 6,279051953.a ise 6,279051953.a/2.a = 3,1395259765
Yüzgen = 100.√2.a.√(1 – cos360/100) = 6,282151816.a ise 6,282151816.a/2.a = 3,141075908
Beşyüzgen = 500.√2.a.√(1 – cos360/500) = 6,283143966.a ise 6,283143966.a/2.a = 3,141571983
Bingen = 1000.√2.a.√(1 – cos360/1000) = 6,283174971.a ise 6,283174971.a/2.a = 3,1415874855
Beşbingen = 5000.√2.a.√(1 – cos360/5000) = 6,283184885.a ise 6,283184885.a/2.a = 3,141592443
Onbingen = 10000.√2.a.√(1 – cos360/10000) = 6,283185132.a ise 6,283185132.a/2.a = 3,141592566
Yukarıdan da anlaşılacağı üzere kenar sayısı olan n sonsuza (∞) doğru giderken bulduğumuz sonuçlar pi sayısının (π) değeri olan 3,141592654…'e doğru yaklaşır ve n sonsuza ulaştığında düzgün çokgenimiz artık bir çembere dönüşmüştür.
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.