Sin 2x Açılımı

Sin 2x'in Açılımı Nedir ?

Sin 2x'in açılımı 2.sin x.cos x'tir.

İspatı

1. Yol

$\text{sin 2x}=\text{sin (x + x)}$

$\boxed{\text{sin (a + b) = sin a.cos b + sin b.cos a}}$

$\text{sin 2x = sin x.cos x + sin x.cos x}$

$\text{sin 2x = 2.sin x.cos x}$

2. Yol

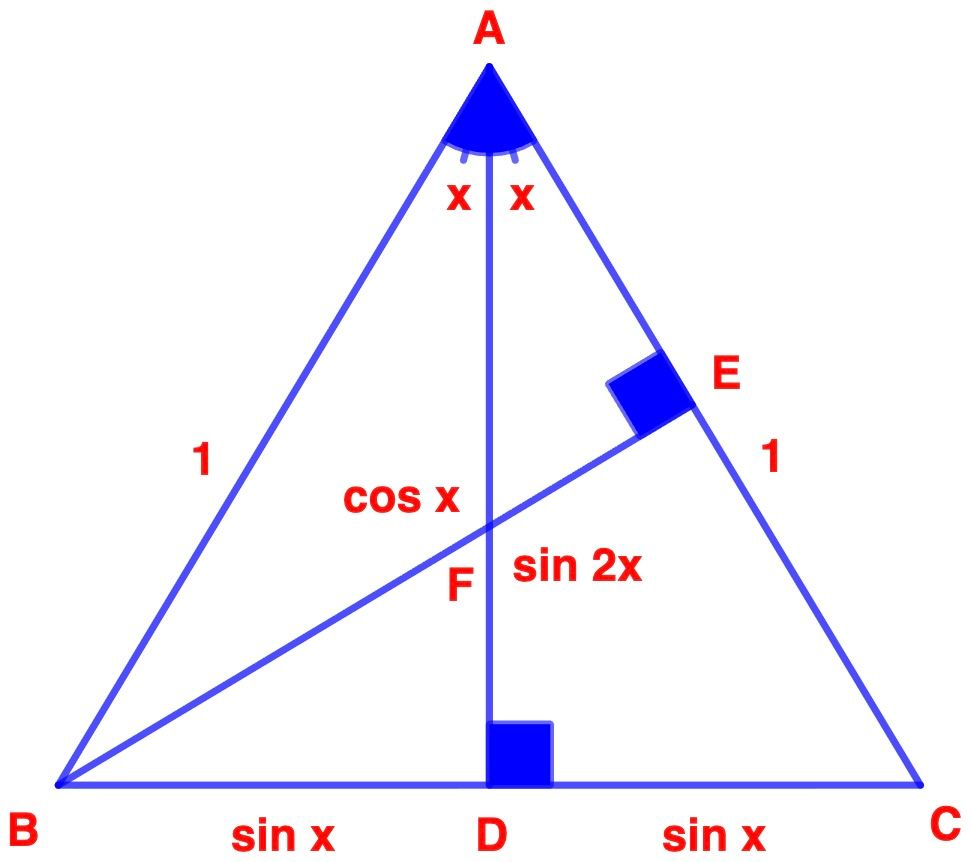
Yukarıdaki şekilde;

$\text{AB = AC = 1}$

$\frac{\text{BD}}{\text{BA}}=\text{sin x}$

$\frac{\text{BD}}{\text{1}}=\text{sin x}$

$\text{BD = 1.sin x}$

$\text{BD = sin x}$

$\frac{\text{CD}}{\text{CA}}=\text{sin x}$

$\frac{\text{CD}}{\text{1}}=\text{sin x}$

$\text{CD = 1.sin x}$

$\text{CD = sin x}$

$\frac{\text{DA}}{\text{BA}}=\text{cos x}$

$\frac{\text{DA}}{\text{1}}=\text{cos x}$

$\text{DA = 1.cos x}$

$\text{DA = cos x}$

$\frac{\text{BE}}{\text{BA}}=\text{sin 2x}$

$\frac{\text{BE}}{\text{1}}=\text{sin 2x}$

$\text{BE = 1.sin 2x}$

$\text{BE = sin 2x}$

$\text{Alan (ABC)}=\frac{\text{AC.BE}}{\text{2}}$

$\text{Alan (ABC)}=\frac{\text{BC.AD}}{\text{2}}$

$\frac{\text{AC.BE}}{\text{2}}=\frac{\text{BC.AD}}{\text{2}}$

$\text{AC.BE}=\text{BC.AD}$

$\text{1.sin 2x}=\text{2sin x.cos x}$

$\text{sin 2x}=\text{2.sin x.cos x}$

3. Yol

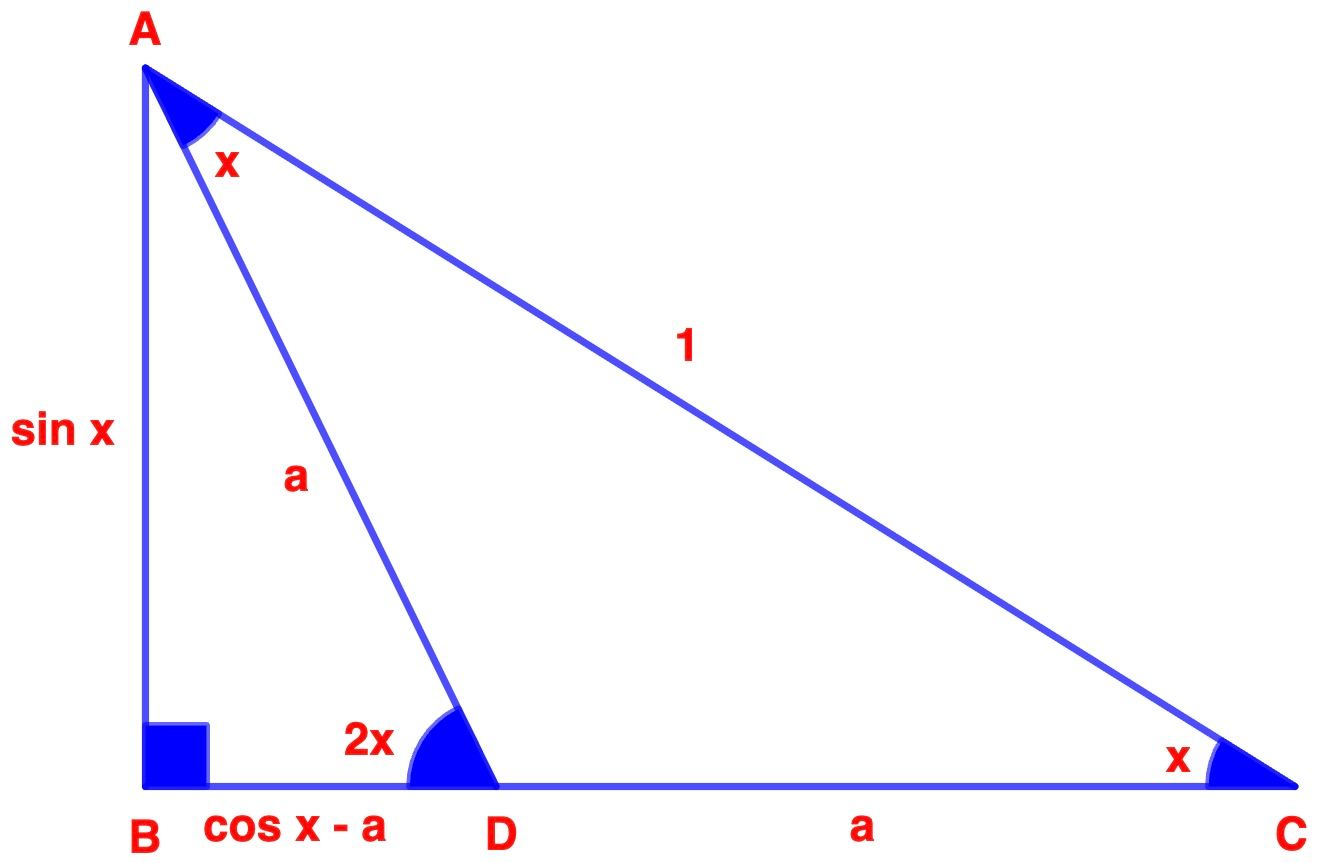
Yukarıdaki şekilde;

$\text{AC = 1}$

$\text{AD = DC = a}$

$\frac{\text{AB}}{\text{AC}}=\text{sin x}$

$\frac{\text{AB}}{\text{1}}=\text{sin x}$

$\text{AB = 1.sin x}$

$\text{AB = sin x}$

$\frac{\text{BC}}{\text{AC}}=\text{cos x}$

$\frac{\text{BC}}{\text{1}}=\text{cos x}$

$\text{BC = 1.cos x}$

$\text{BC = cos x}$

$\text{BD = BC - DC}$

$\text{BD = cos x - a}$

ABD üçgeni için Pisagor Bağıntısı'nı yazarsak;

$\text{(AB)² + (BD)² = (AD)²}$

$\text{sin² x + (cos x - a)² = a²}$

$\text{sin² x + cos² x - 2.cos x.a + a² = a²}$

$\boxed{\text{sin² x + cos² x = 1}}$

$\text{1 - 2.cos x.a + a² = a²}$

$\text{1 - 2.cos x.a = a² - a²}$

$\text{1 - 2.cos x.a = 0}$

$\text{-2.cos x.a = -1}$

$\text{a}=\frac{\text{-1}}{\text{-2cos x}}$

$\text{a}=\frac{\text{1}}{\text{2cos x}}$

ABD üçgeni için sinüs oranını yazarsak;

$\frac{\text{sinx}}{\text{a}}=\text{sin 2x}$

$\frac{\text{sinx}}{\frac{\text{1}}{\text{2cos x}}}=\text{sin 2x}$

$\text{sin x.2cos x = sin 2x}$

$\text{2.sin x.cos x = sin 2x}$