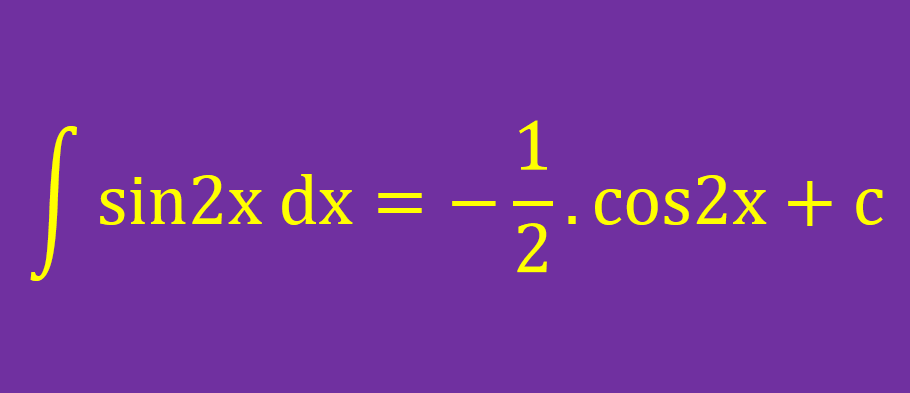Sin2x İntegrali





Sin2x İntegrali Nedir?



sin2x'in İntegrali -1/2.cos2x+c'ye eşittir.



İspat 1



∫ sin2x dx = ?

2x = u

d(2x) =du (Eşitliği her iki tarafının da diferansiyelini alırız)



Diferansiyel Alma İşlemi

y = f(x)

dy = df(x)

dy = f(x)'dx

dy/dx = f(x)'

dy/dx = y' = f(x)' olur.



d(2x) =du

(2x)'dx = du

2dx = du

dx = du/2 olur.



2x = u ve dx = du/2



∫ sin2x dx = ∫ sinu du/2

∫ sin2x dx = 1/2.∫ sinu du

∫ sinx dx = -cosx+c olduğunu biliyoruz.

∫ sin2x dx = 1/2.∫ sinu du

∫ sin2x dx = -1/2.cosu+c

∫ sin2x dx = -1/2.cos2x+c olur.



İspat 2



∫ sin2x dx = ?

sin2x = 2.sinx.cosx

∫ sin2x dx = ∫ 2.sinx.cosx dx

sinx = u

d(sinx) = du

(sinx)'dx = du

cosxdx = du



sinx = u ve cosx dx = du



∫ sin2x dx = ∫ 2.u.du

∫ sin2x dx = 2.u²/2 + c

∫ sin2x dx = u² + c

∫ sin2x dx = sin²x + c olur.