Sinüs Alan Formülü (Sinüslü Alan Formülü)

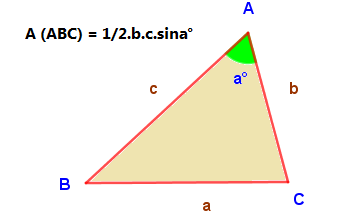
Bir üçgenin herhangi iki kenarının uzunluğunu ve bu iki kenarı arasındaki açının ölçüsünü biliyorsak, o üçgenin alanını aşağıdaki şekildeki gibi hesaplayabiliriz.

Yukarıda iki kenarı ve bir açısı bilinen ABC üçgeninin alanı; A (ABC) = 1/2.b.c.sina°'dır.

Sinüs Alan Formülü İspatı

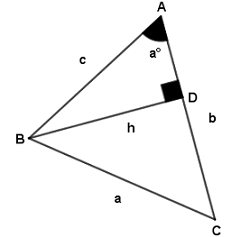
Yukarıdaki ABC üçgenin alanı;

A (ABC) = b.h/2'dir.

ABD dik üçgeninde sina° = h/c olur.

h/c = sina° ise h = c.sina° olur.

Yukarıdaki alan formülünde h gördüğümüz yere c.sina° yazalım.

A (ABC) = b.c.sina°/2 = 1/2.b.c.sina° olur.

Aynı formülü üçgenin diğer kenarları ve açıları için uygularsak;

A (ABC) = 1/2.a.c.sinb°

A (ABC) = 1/2.a.b.sinc° olur.

Önemli ! a/sina° = b/sinb° = c/sinc°'dir.

İspatı

1/2.b.c.sina° = 1/2.a.c.sinb° = 1/2.a.b.sinc°

b.c.sina° = a.c.sinb° = a.b.sinc°

b.c.sina°/a.b.c = a.c.sinb°/a.b.c = a.b.sinc°/a.b.c

sina°/a = sinb°/b = sinc°/c, buradan;

a/sina° = b/sinb° = c/sinc° olur.

Örnek 1: Bir ABC üçgeninde a kenarının uzunluğu 8 cm, b kenarının uzunluğu 5 cm ve a ile b kenarı arasında kalan C açısının ölçüsü 30° ise bu üçgenin alanı ne kadardır ?

A (ABC) = 1/2.a.b.sinC

A (ABC) = 1/2.8.5.sin30°

(sin30° = 1/2 = 0,5)

A (ABC) = 1/2.8.5.0,5

A (ABC) = 1/2.20

A (ABC) = 10 cm² olur.

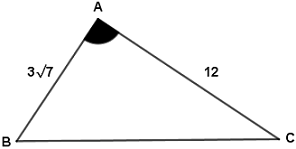
Örnek 2:

Yukarıdaki üçgenin alanı 18√7 ise, A açısının ölçüsünün değerin bulunuz.

A (ABC) = 1/2.b.c.sinA

18√7 = 1/2.12.3√7.sinA

18√7 = 1/2.36√7.sinA

18√7 = 18√7.sinA

1 = sinA

(sin90° = 1)

A = 90 olur.