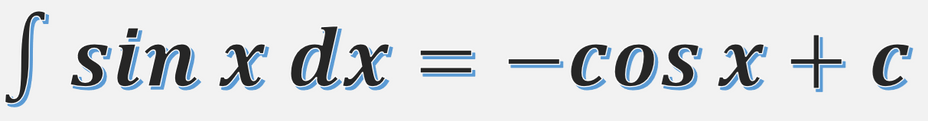Sin x'in integrali -cos x'tir.
Sin x'in İntegrali Nedir ? Sin x'in integrali -cos x'tir.
∫ s in x d x = − cos x + c
Sin x'in İntegralini Bulma 1. Yol
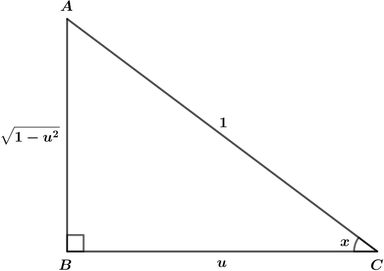
Yukarıdaki ABC dik üçgeninde;
s in x = 1 1 − u 2 = 1 − u 2
cos x = 1 u = u
∫ s in x d x = ?
s in x = 1 − u 2
d ( s in x ) = d ( 1 − u 2 )
( s in x ) ′ d x = ( 1 − u 2 ) ′ d u
( s in x ) ′ = cos x
f ( x ) = u ( x ) ⇒ f ′ ( x ) = 2 u ( x ) u ′ ( x )
cos x d x = 2 1 − u 2 ( 1 − u 2 ) ′ d u
u d x = 2 1 − u 2 − 2 u d u
d x = 2 u 1 − u 2 − 2 u d u
∫ s in x d x = ∫ 1 − u 2 . 1 − u 2 − d u
∫ s in x d x = − ∫ d u
∫ s in x d x = − u + c
∫ s in x d x = − cos x + c
2. Yol ∫ s in x d x = ?
s in 2 x = 2. s in x . cos x
∫ s in x d x = ∫ 2. s in 2 x . cos 2 x d x
s in 2 x = u
d ( s in 2 x ) = d u
( s in 2 x ) ′ d x = d u
( s in a x ) ′ = a . cos a x
2 1 cos 2 x d x = d u
cos 2 x d x = 2 d u
∫ s in x d x = ∫ 2. u .2 d u
∫ s in x d x = ∫ 4 u d u
∫ s in x d x = 2 4 u 2 + c
∫ s in x d x = 2 u 2 + c
∫ s in x d x = 2 s i n 2 2 x + c
1 − 2 s i n 2 x = cos 2 x
1 − 2 s i n 2 2 x = cos x
− ( 1 − 2 s i n 2 2 x ) = − cos x
2 s i n 2 2 x − 1 = − cos x
c ∈ R , c = − 1 ⇒ ∫ s in x d x = 2 s i n 2 2 x − 1
∫ s in x d x = − cos x
3. Yol s in x = x − 3 ! x 3 + 5 ! x 5 − 7 ! x 7 + 9 ! x 9 − ...
cos x = 1 − 2 ! x 2 + 4 ! x 4 − 6 ! x 6 + 8 ! x 8 − ...
∫ s in x d x = ∫ ( x − 3 ! x 3 + 5 ! x 5 − 7 ! x 7 + 9 ! x 9 − ... ) d x
∫ s in x d x = ( 2 x 2 − 4.3 ! x 4 + 6.5 ! x 6 − 8.7 ! x 8 + 10.9 ! x 10 − ... ) + c
∫ s in x d x = ( 2 ! x 2 − 4 ! x 4 + 6 ! x 6 − 8 ! x 8 + 10 ! x 10 − ... ) + c
c ∈ R , c = − 1 ⇒ ∫ s in x d x = ( 2 ! x 2 − 4 ! x 4 + 6 ! x 6 − 8 ! x 8 + 10 ! x 10 − ... ) − 1
∫ s in x d x = − 1 + 2 ! x 2 − 4 ! x 4 + 6 ! x 6 − 8 ! x 8 + 10 ! x 10 − ...
∫ s in x d x = − ( 1 − 2 ! x 2 + 4 ! x 4 − 6 ! x 6 + 8 ! x 8 − 10 ! x 10 + ... )
∫ s in x d x = − cos x