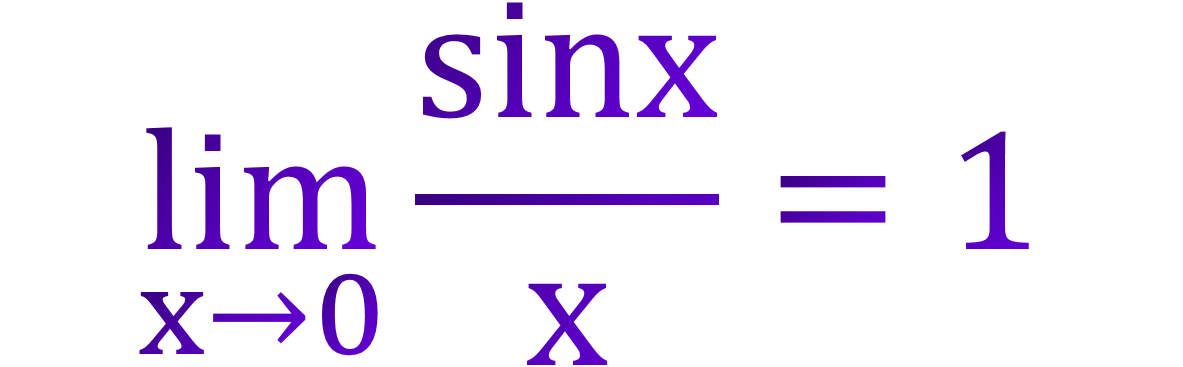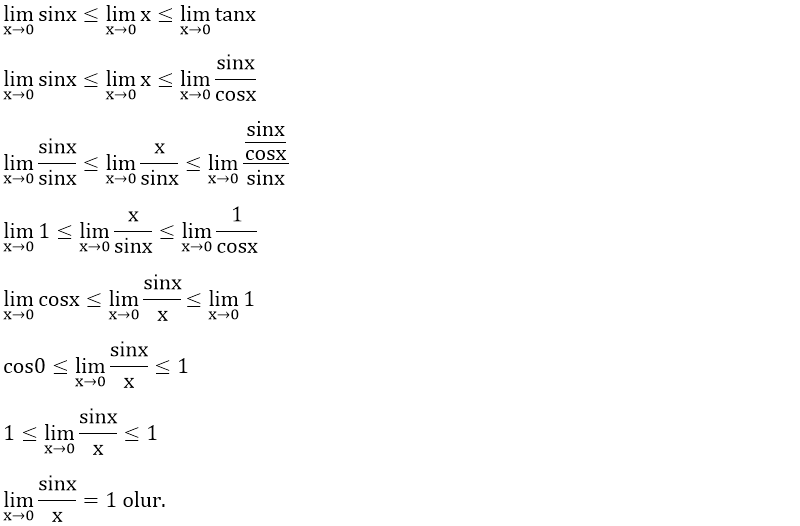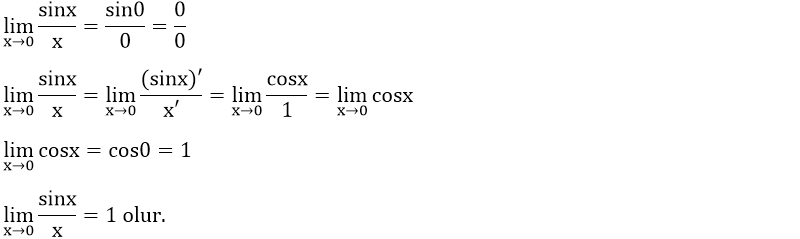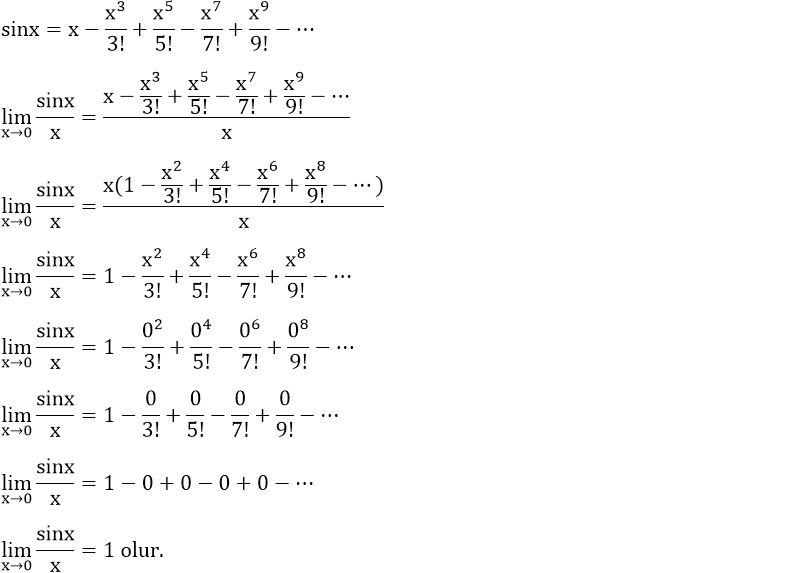sinx / x (sinx / x limit)

sinx/x Fonksiyonunun x = 0 noktasındaki limiti 1'e eşittir. Bunu aşağıdaki şekildeki gibi 3 farklı yoldan ispatlayabiliriz.

1. Yol

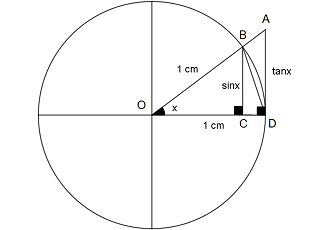
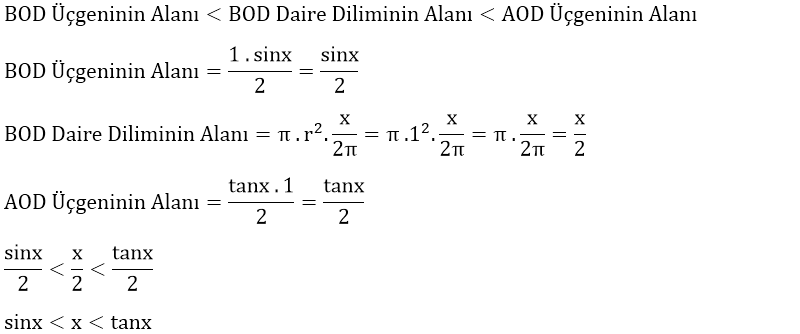
Yukarıdaki şekildeki çember, yarıçapı 1 birim olan (r = 1) bir birim çemberdir. Şekle dikkatlice bakıldığında BOD üçgenin alanının BOD daire diliminin alanından, BOD daire diliminin alanının ise AOD üçgeninin alanından daha küçük olduğu kolaylıkla anlaşılabilir.

Eğer x açısının ölçüsünü giderek küçültürsek bu üç şeklin alanı da giderek küçülecek ve x açısının ölçüsü 0° olduğunda bu üç şeklin alanı da 0'a eşit olacaktır. Bu eşitliği limit alma ve eşitsizlik kurallarını da kullanarak aşağıdaki şekildeki gibi gösterebiliriz.

Şimdi işimiz sadece limit halindeki yukarıdaki eşitsizliğin çözüm kümesini bulmaya kaldı.

Önemli !

İspat

2. Yol

L'Hôpital (okunuşu: löpital) kuralından faydalanarak da x 0'a doğru giderken sinx/x'in limitinin 1'e eşit olduğunu ispatlayabiliriz.

İspat

3. Yol

sinx'in sonsuz seri şeklindeki açılımından faydlanarak da sinx/x'in x = 0 noktasındaki limitinin 1'e eşit olduğunu ispatlayabiliriz.

İspat