Ters Fonksiyon

Fonksiyon Nedir?

En basit tanımıyla verilmiş olan sayılarla ne yapılacağını gösteren kurala fonksiyon denir.

1 → 2

2 → 4

3 → 6

4 → 8

Yukarıda ok işaretinin sağ tarafındaki sayılar sol tarafındaki sayıların hep iki katıdır. Bu bize sol taraftaki her hangi bir sayının iki katını alarak sağ tarafa yaz demektir. Bunu bir kural şeklinde veya kurala dönüştürerek yazmak istersek sol taraftaki her hangi bir x sayısının iki katı sağ tarafta 2x'e karşılık gelir.

x → 2x

x'e fonksiyonun tanım kümesi 2x'e ise değer kümesi denir. Değer kümesi çoğunlukla "y" veya "f(x)" şeklinde gösterilir.

x → 2x

x → y

x → f(x)

y = f(x) = 2x

Fonksiyonları göstermenin yollarından biri Venn şeması diğer ise grafik yöntemidir.

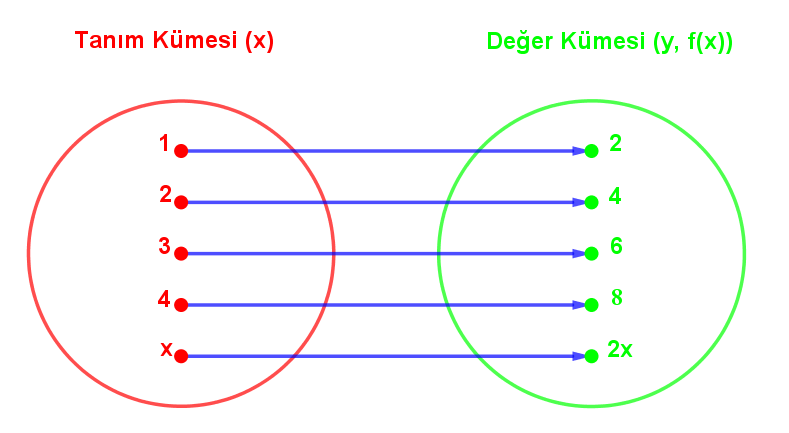
Venn Şeması ile Fonksiyonları Gösterme

Yukarıdaki şekilde y = f(x) = 2x fonksiyonunun Venn şeması şeklindeki gösterilişini görmektesiniz.

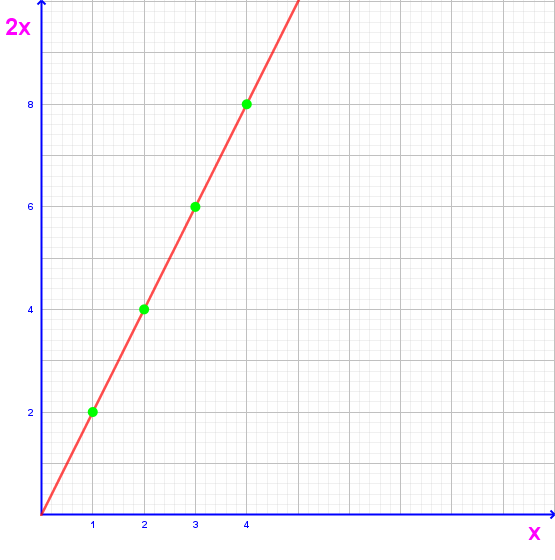
Grafik ile Fonksiyonları Gösterme

Yukarıdaki şekilde y = f(x) = 2x fonksiyonunun grafik şeklindeki gösterilişini görmektesiniz.

Ters Fonksiyon Nedir?

Tanım kümesinin değer kümesi, değer kümesinin de tanım kümesi yerine geçtiği (olduğu) fonksiyonlara ters fonksiyon denir.

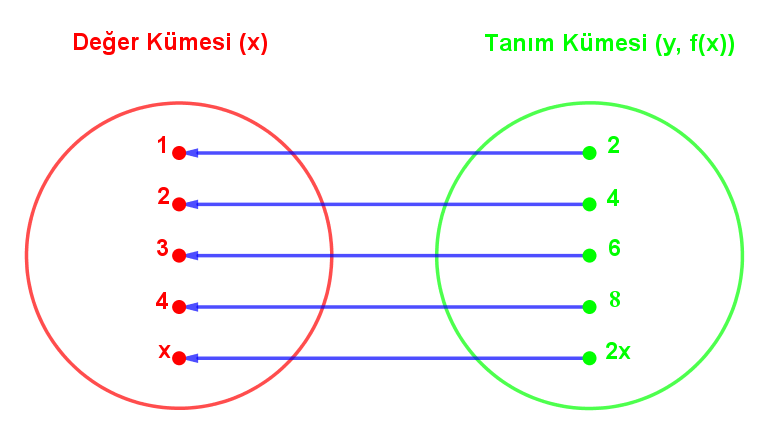
Yukarıda Venn şeması şeklinde göstermiş olduğumuz y = f(x) = 2x fonksiyonunda tanım kümesi ile değer kümesinin yerini değiştirerek ters fonksiyon olayını anlatmaya çalışalım.

2 → 1

4 → 2

6 → 3

8 → 4

2x → x

x → ?

Yukarıda ok işaretinin sağ tarafındaki sayılar sol tarafındaki sayıların hep yarısıdır. Bu bize sol taraftaki her hangi bir sayının yarısını (1/2'sini) alarak sağ tarafa yaz demektir. Bunu bir kural şeklinde veya kurala dönüştürerek yazmak istersek sağ taraftaki her hangi bir x sayısının yarısı sol tarafta x/2'ye karşılık gelir.

Buradan 2x fonksiyonunun ters fonksiyonunun x/2 olduğunu söyleyebiliriz.

Bir Fonksiyonun Tersi Nasıl Bulunur?

Yukarıdaki şekildeki Venn şemasında 2 1'e, 4 2'ye, 6 3'e, 8 4'e ve 2x x'e gitmektedir. Peki tanım kümesinde 2x değil de bir x değeri olsaydı değer kümesinde nereye giderdi? Bu sorunun cevabını bulduğumuz an f(x) fonksiyonumuzun tersini de bulmuş oluruz.

Tanım kümesindeki 2x'te x yerine hangi değer gelmelidir ki bizi değer kümesinde x'e götürsün.

2x → x

2x ifadesindeki x yerine gelecek değeri u ile gösterelim.

2u = x

u = x/2 olur.

Bunun anlamı tanım kümesinde bir x değeri olsaydı bu bizi değer kümesinde x/2'ye götürürdü demektir.

O zaman y = f(x) = 2x fonksiyonunun tersi olan fonksiyonun genel denklemi x/2'dir.

Bir fonksiyonun tersinin olabilmesi için fonksiyonun kendisinin birebir örten olması gerekir.

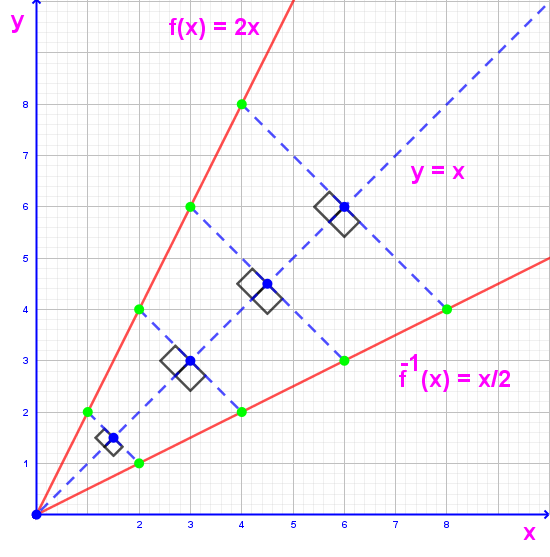
Ters Fonksiyonun Grafiği

Örnek

y = f(x) = 2x + 3 fonksiyonunun tersi nedir?

Çözüm

T → D

0 → 3

1 → 5

2 → 7

3 → 9

4 → 11

x → 2x + 3

Ters fonksiyonda tanım kümesi ile değer kümesi yer değiştirir. Tanım kümesi değer kümesi olurken değer kümesi ise tanım kümesi olur.

T → D

3 → 0

5 → 1

7 → 2

9 → 3

11 → 4

2x + 3 → x

x → ?

Tanım kümesindeki 2x + 3'te x yerine hangi değer gelmelidir ki bizi değer kümesinde x'e götürsün.

x'in alacağı değere u diyelim.

2u + 3 = x

2u = x - 3

u = (x - 3)/2 olur.

Bunun anlamı tanım kümesinde bir x değeri olsaydı bu bizi değer kümesinde (x - 3)/2'ye götürürdü demektir.

O zaman y = f(x) = 2x + 3 fonksiyonunun tersi olan fonksiyonun genel denklemi (x - 3)/2'dir.

Bir Fonksiyonun Tersini Bulmanın Kolay Yolu

y = f(x) şeklindeki bir fonksiyonun tersi bulunurken x yerine y, y yerine x yazılır ve y yalnız bırakırız.

Örnek

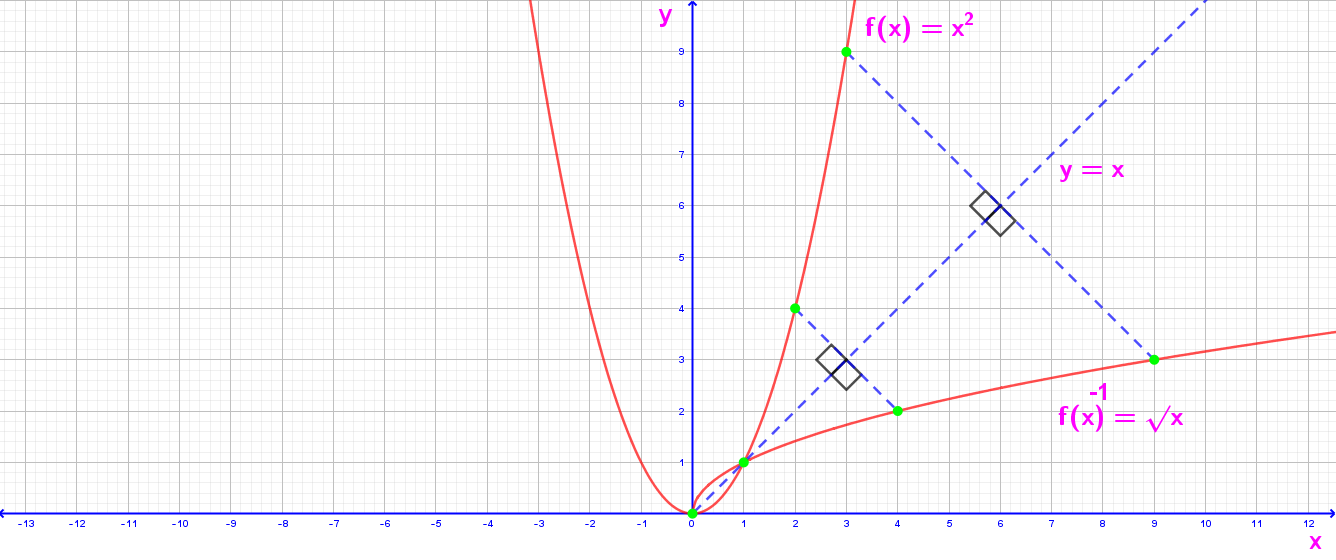
y = f(x) = x² fonksiyonunun ters fonksiyonu nedir?

Çözüm

y = x²

x = y² (x ile y yer değiştirir)

y² = x

√y² = √x

y = √x olur.

Örnek

y = f(x) = 5x + 3 fonksiyonunun tersi nedir?

Çözüm

y = 5x + 3

x = 5y + 3

5y + 3 = x

5y = x - 3

y = (x - 3)/5 olur.

Ters Fonksiyon Bulma Kuralları

1. f(x) = x + a şeklindeki bir fonksiyonun tersi x - a'dır.

2. f(x) = x - a şeklindeki bir fonksiyonun tersi x + a'dır.

3. f(x) = ax + b şeklindeki bir fonksiyonun tersi (x - b)/a'dır.

4. f(x) = ax - b şeklindeki bir fonksiyonun tersi (x + b)/a'dır.

5. f(x) = ax şeklindeki bir fonksiyonun tersi x/a'dır.

6. f(x) = x/a şeklindeki bir fonksiyonun tersi ax'tir.

7. f(x) = (ax + b)/(cx + d) şeklindeki bir fonksiyonun tersi (-dx + b)/(cx - a)'dır.