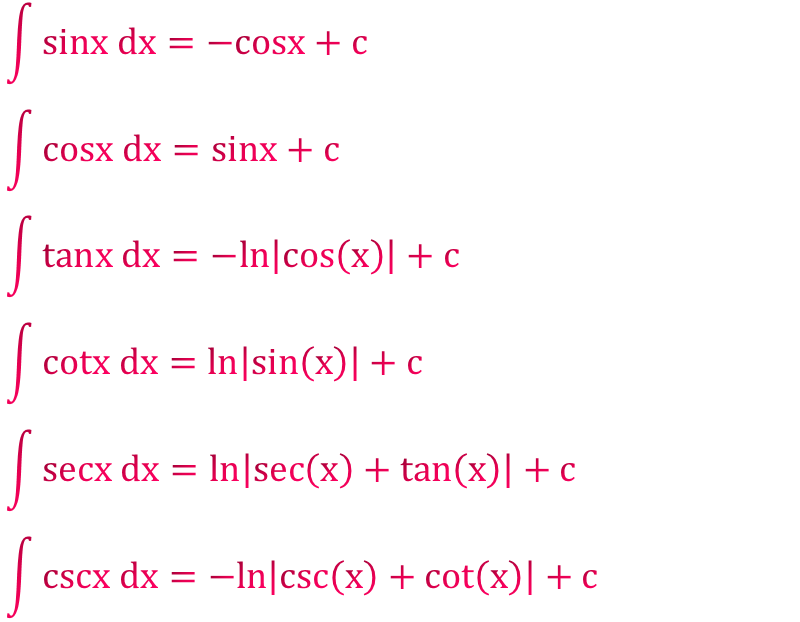trigonometrik fonksiyonların integrali

1. Sinüs İntegrali

1. ∫ sin(x) dx = -cos(x) + c

2. ∫ sin(ax + b) dx = -1/a . cos(ax + b) + c (a ≠ 0)

3. ∫ dx/sin(x) = ln|tan(x/2)| + c

4. ∫ dx/sin(ax + b) = 1/a . ln|tan(ax + b/2)| + c (a ≠ 0)

2. Kosinüs İntegrali

1. ∫ cos(x) dx = sin(x) + c

2. ∫ cos(ax + b) dx = 1/a . sin(ax + b) + c (a ≠ 0)

3. ∫ dx/cos(x) = ln|tan(x/2 + π/4)| + c

4. ∫ dx/cos(ax + b) = 1/a . ln|tan[(ax + b)/2 + π/4]| + c (a ≠ 0)

3. Tanjant İntegrali

1. ∫ tan(x) dx = -ln|cos(x)| + c = ln|sec(x)| + c

2. ∫ tan(ax + b) dx = -1/a . ln|cos(ax + b)| + c = 1/a . ln|sec(ax + b)| + c (a ≠ 0)

3. ∫ dx/tan(x) = ln|sinx| + c

4. ∫ dx/tan(ax + b) = 1/a . ln|sin(ax + b)| + c (a ≠ 0)

4. Kotanjant İntegrali

1. ∫ cot(x) dx = ln|sin(x)| + c

2. ∫ cot(ax + b) dx = 1/a . ln|sin(ax + b)| + c (a ≠ 0)

3. ∫ dx/cot(x) = -ln|cos(x)| + c = ln|sec(x)| + c

4. ∫ dx/cot(ax + b) = -1/a . ln|cos(ax + b)| + c = 1/a . ln|sec(ax + b)| + c (a ≠ 0)

5. Sekant İntegrali

1. ∫ sec(x) dx = ln|sec(x) + tan(x)| + c

2. ∫ sec(ax + b) dx = 1/a . ln|sec(ax + b) + tan(ax + b)| + c (a ≠ 0)

3. ∫ dx/sec(x) = sin(x) + c

4. ∫ dx/sec(ax + b) = 1/a . sin(ax + b) + c (a ≠ 0)

6. Kosekant İntegrali

1. ∫ csc(x) dx = -ln|csc(x) + cot(x)| + c

2. ∫ csc(ax) dx = -1/a . ln|csc(ax + b) + cot(ax + b)| + c (a ≠ 0)

3. ∫ dx/csc(x) = -cos(x) + c

4. ∫ dx/csc(ax + b) = -1/a . cos(ax + b) + c (a ≠ 0)