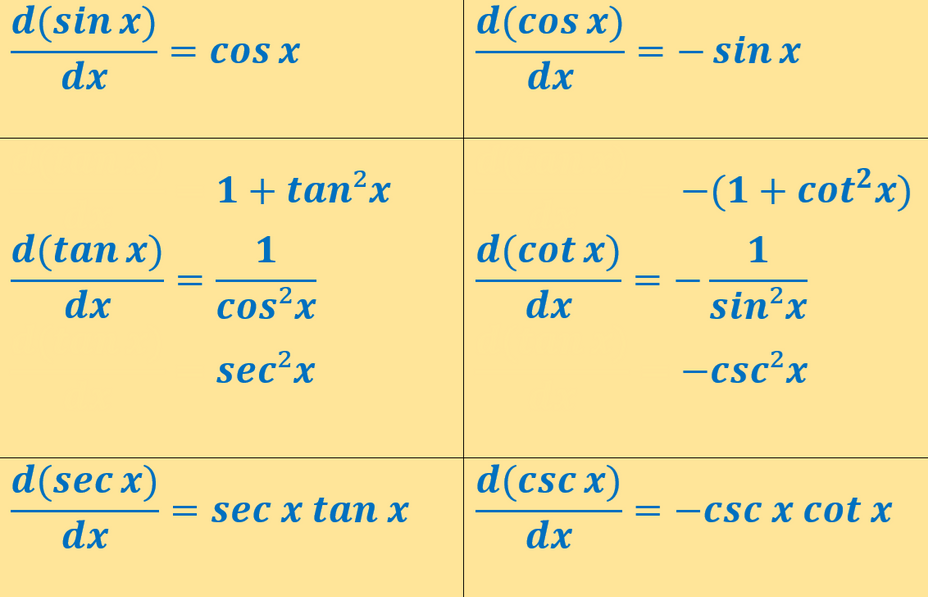Trigonometrik Fonksiyonların Türevi

Pow

@pow

May 02, 2025

Sin x, cos x, tan x, cot x, sec x ve csc x fonksiyonlarının türevi.

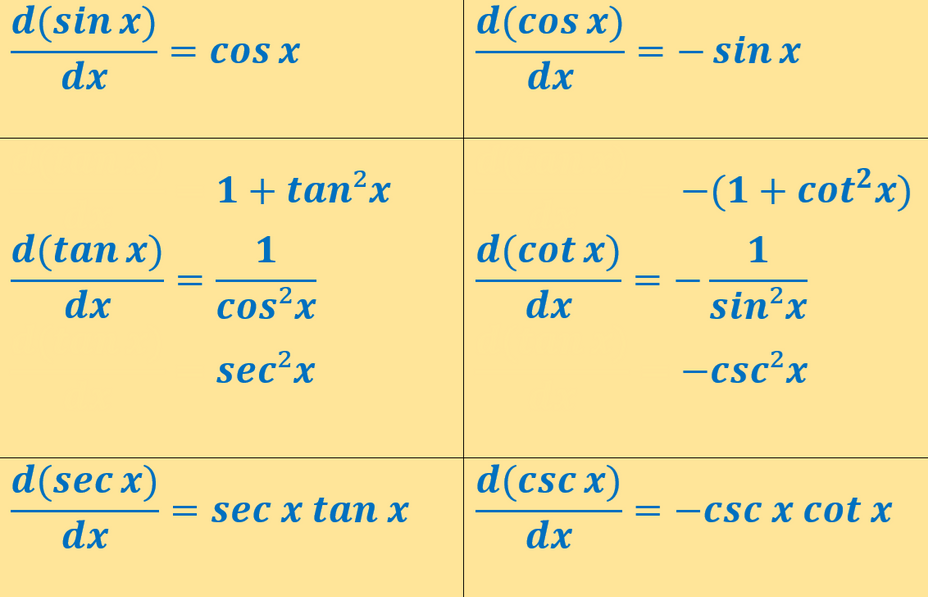
trigonometrik fonksiyonların türevi.png

1. Sin x'in Türevi

Sin x'in türevi cos x'tir.

$(s in x)^{'} = cos x$

$(s in a x)^{'} = a . cos a x$

$(s in u)^{'} = u^{'} . cos u$

Soru

$f (x) = s in (x^{2} + 3 x - 5) \Rightarrow f^{'} (x) = ?$

Cevap

$(s in u)^{'} = u^{'} . cos u$

$[s in (x^{2} + 3 x - 5)]^{'} = (x^{2} + 3 x - 5)^{'} . cos (x^{2} + 3 x - 5)$

$[s in (x^{2} + 3 x - 5)]^{'} = (2 x + 3) . cos (x^{2} + 3 x - 5)$

2. Cos x'in Türevi

Cos x'in türevi -sin x'tir.

$(cos x)^{'} = - s in x$

$(cos a x)^{'} = - a . s in a x$

$(cos u)^{'} = - u^{'} . s in u$

Soru

$f (x) = cos (- 3 x^{3} + 5 x) \Rightarrow f^{'} (x) = ?$

Cevap

$(cos u)^{'} = - u^{'} . s in u$

$[cos (- 3 x^{3} + 5 x)]^{'} = - (- 3 x^{3} + 5 x)^{'} . s in (- 3 x^{3} + 5 x)$

$[cos (- 3 x^{3} + 5 x)]^{'} = - (- 3.3. x^{2} + 5) . s in (- 3 x^{3} + 5 x)$

$[cos (- 3 x^{3} + 5 x)]^{'} = - (- 9 x^{2} + 5) . s in (- 3 x^{3} + 5 x)$

$[cos (- 3 x^{3} + 5 x)]^{'} = (9 x^{2} - 5) . s in (- 3 x^{3} + 5 x)$

3. Tan x'in Türevi

Tan x'in türevi 1+tan² x'tir.

$(t an x)^{'} = 1 + t a n^{2} x$

$(t an a x)^{'} = a . (1 + t a n^{2} a x)$

$(t an u)^{'} = u^{'} . (1 + t a n^{2} u)$

Soru

$f (x) = t an (3 x + 5) \Rightarrow f^{'} (x) = ?$

Cevap

$(t an u)^{'} = u^{'} . (1 + t a n^{2} u)$

$[t an (3 x + 5)]^{'} = (3 x + 5)^{'} . [1 + t a n^{2} (3 x + 5)]$

$[t an (3 x + 5)]^{'} = 3. [1 + t a n^{2} (3 x + 5)]$

$[t an (3 x + 5)]^{'} = 3.1 + 3. t a n^{2} (3 x + 5)$

$[t an (3 x + 5)]^{'} = 3 + 3. t a n^{2} (3 x + 5)$

4. Cot x'in Türevi

Cot x'in türevi -(1+cot² x)'tir.

$(co t x)^{'} = - (1 + co t^{2} x)$

$(co t a x)^{'} = - a . (1 + co t^{2} a x)$

$(co t u)^{'} = - u^{'} . (1 + co t^{2} u)$

Soru

$f (x) = co t x^{2} \Rightarrow f^{'} (x) = ?$

Cevap

$(co t u)^{'} = - u^{'} . (1 + co t^{2} u)$

$(co t x^{2})^{'} = - (x^{2})^{'} . (1 + co t^{2} x^{2})$

$(co t x^{2})^{'} = - 2 x . (1 + co t^{2} x^{2})$

$(co t x^{2})^{'} = - 2 x .1 - 2 x . co t^{2} x^{2}$

$(co t x^{2})^{'} = - 2 x - 2 x . co t^{2} x^{2}$

5. Sec x'in Türevi

Sec x'in türevi sec x.tan x'tir.

$(sec x)^{'} = sec x . t an x$

$(sec a x)^{'} = a . sec a x . t an a x$

$(sec u)^{'} = u^{'} . sec u . t an u$

Soru

$f (x) = sec 3 x \Rightarrow f^{'} (x) = ?$

Cevap

$(sec u)^{'} = u^{'} . sec u . t an u$

$(sec 3 x)^{'} = (3 x)^{'} . sec 3 x . t an 3 x$

$(sec 3 x)^{'} = 3. sec 3 x . t an 3 x$

6. Csc x'in Türevi

Csc x'in türevi -csc x.cot x'tir.

$(csc x)^{'} = - csc x . co t x$

$(csc a x)^{'} = - a . csc a x . co t a x$

$(csc u)^{'} = - u^{'} . csc u . co t u$

Soru

$f (x) = csc 4 x \Rightarrow f^{'} (x) = ?$

Cevap

$(csc u)^{'} = - u^{'} . csc u . co t u$

$(csc 4 x)^{'} = - (4 x)^{'} . csc 4 x . co t 4 x$

$(csc 4 x)^{'} = - 4. csc 4 x . co t 4 x$

# türev # trigonometri # matematik

Comments

There are no records on the list.