Üçgenin İç Açıları Toplamı (Üçgenin İç Açıları Toplamı Kaçtır?)

Pow
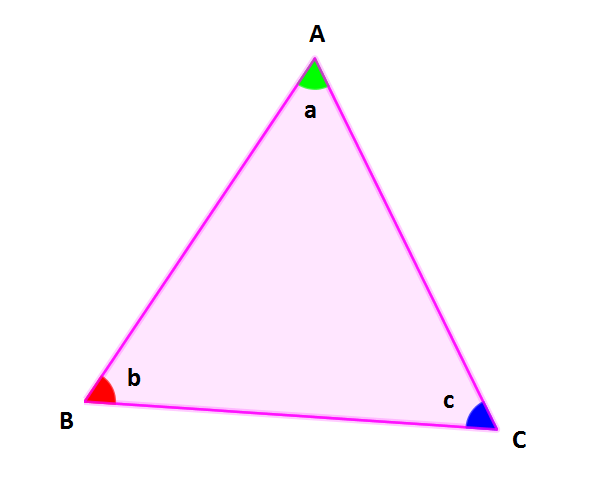
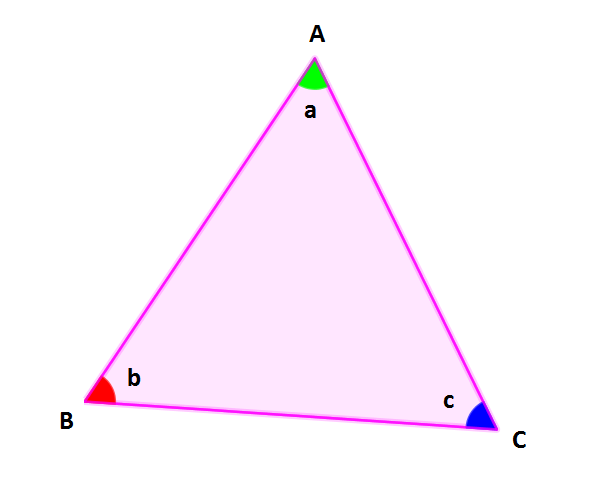
Üçgenin İç Açıları Toplamı Neden 180 Derecedir? Bir üçgenlerde iç açıların toplamı 180°'dir. Yukarıdaki ABC üçgeninde; m (A) + m (B) + m (C) = a + b + c = 18
Üçgenin İç Açıları Toplamı Neden 180 Derecedir?
Bir üçgenlerde iç açıların toplamı 180°'dir. Yukarıdaki ABC üçgeninde;
m (A) + m (B) + m (C) = a + b + c = 180° olur.
Bir üçgenin iç açılarının toplamının 180° olduğunu çeşitli yollardan ispatlayabiliriz.
1. Yol
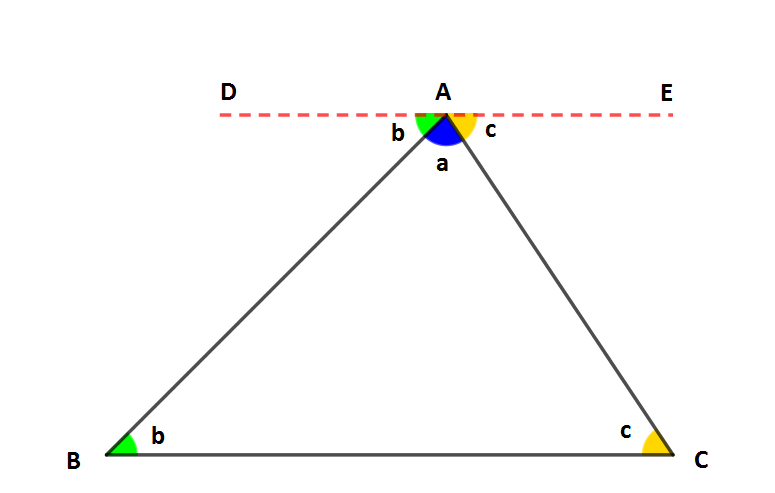
Yukarıdaki ABC üçgeninde kırmızı kesikli çizgiler ile gösterdiğimiz DE doğru paçası BC kenarına paraleldir.
Yani; [DE] // |BC|'dir.
Geometri derslerinde açı konusunu işlerken öğrendiğimiz bilgilere göre DAB ile ABC ve EAC ile BCA açıları iç ters açılardır. Hepimizin bildiği üzere iç ters açıların ölçüleri birbirine eşittir.
Yani; m (DAB) = m (ABC) = b ve m (EAC) = m (BCA) = c olur.
şekildeki DAE doğru parçası üzerinde oluşan açı bir doğru açıdır ve bir doğru açının ölçüsü de 180°'dir.
m (DAE) = 180 = b + a + c = a + b + c olur.
(a + b + c)'nin toplamı olan 180 üçgenin iç açılarının toplamına eşittir.
Böylelikle bir üçgenin iç açılarının toplamının 180 derece olduğunu bu şekilde ispatlamış olduk.
2. Yol
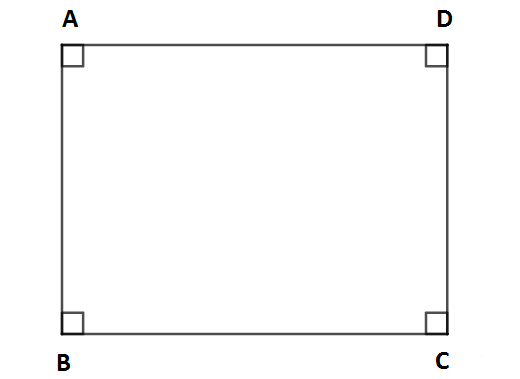
Yukarıdaki ABCD dikdörtgeninde A ve C veya B ve D köşelerini birleştiren bir doğru parçası çizelim. Biz B ve D köşelerini birleştiren bir doğru parçası çizmeye tercih ettik.
[BD] doğru parçası dikdörtgeni ikiye ayırarak ABD ve BCD olmak üzere iki tane üçgen oluşmasını sağlar.
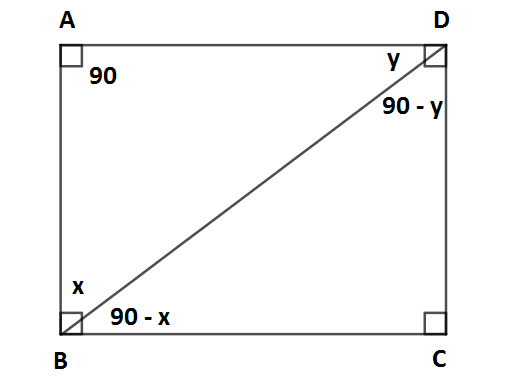
ABD üçgenin iç açılarını toplamı:
m (A) + m (B) + m (D) = 90 + x + y (1. Denklem)
BCD üçgenin iç açılarını toplamı:
m (B) + m (C) + m (D) = 90 - x + 90 + 90 - y = 90 + 90 + 90 - x - y = 270 - (x + y) (2. Denklem)
[AD] doğru parçası [BC] doğru parçasına paralel olduğu için [AD] // [BC]
m (ADB) = m (DBC) ve y = 90 - x olur.
1. Denklem de y gördüğümüz yere 90 - x yazalım.
m (A) + m (B) + m (D) = 90 + x + y
m (A) + m (B) + m (D) = 90 + x + 90 - x
m (A) + m (B) + m (D) = 90 + 90 + x - x
m (A) + m (B) + m (D) = 180 + 0 = 180 olur.
Gerçekten de ABD üçgenin iç açılarını toplamı 180° olarak çıktı.
Şimdi de 2. denklemimiz de y gördüğümüz yere 90 - x yazalım.
m (B) + m (C) + m (D) = 270 - (x + y)
m (B) + m (C) + m (D) = 270 - (x + 90 - x)
m (B) + m (C) + m (D) = 270 - (x - x + 90)
m (B) + m (C) + m (D) = 270 - (0 + 90)
m (B) + m (C) + m (D) = 270 - (90)
m (B) + m (C) + m (D) = 270 - 90
m (B) + m (C) + m (D) = 180
Gerçekten de BCD üçgenin iç açılarını toplamı 180° olarak çıktı.
3. Yol
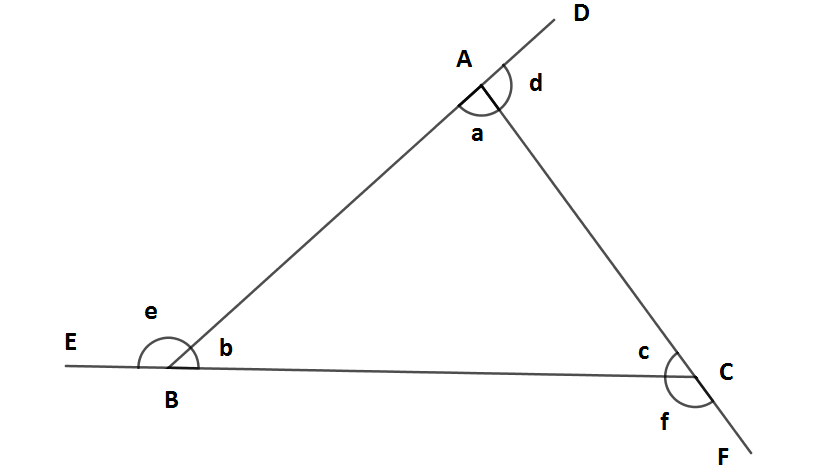
Yukarıdaki ABC üçgeninde üç tane doğru açı bulunmaktadır. Doğru açı hepinizin geometri derslerinden bildiği üzere bir doğru üzerinde bulunan ve ölçüsü 180° olan açıdır.
Birde şunu hatırlatmakta fayda var bütün çokgenlerin üçgen, dörtgen, beşgen, altıgen v.b. hepsinin dış açılarının toplamı her zaman için 360°'dir.
Şimdi ispatımıza geçelim.
a + d = 180
b + e = 180
c + f = 180
d + e + f = 360 (dış açıların toplamı)
(a + d) + (b + e) + (c + f) = 180 + 180 + 180 = 540
(a + b + c) + (d + e + f) = 540
(a + b + c) + 360 = 540
a + b + c = 540 - 360
a + b + c = 180 (iç açıların toplamı)
4. Yol
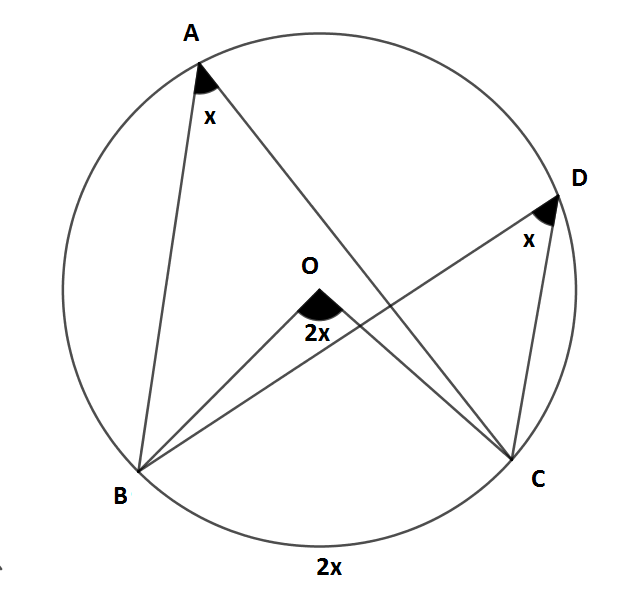
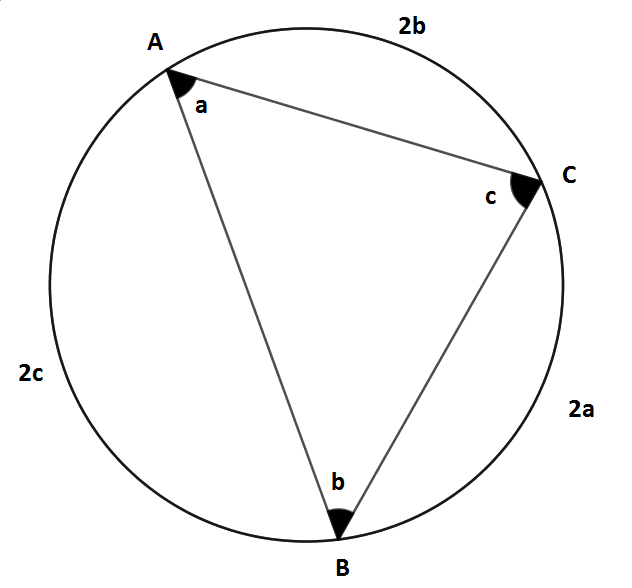
Bir çemberde merkez açı gördüğü yayın ölçüsüne ve çevre açı da gördüğü yayın ölçüsünün yarısına eşittir.
Yukarıdaki çemberde;
m (A) = a, m (B) = b, m (C) = c ve m (BC) = 2a, m (CA) = 2b, m (AB) = 2c'dir.
Şimdi tüm yayların ölçülerini toplayalım
m (BC) + m (CA) + m (AB) = 2a + 2b + 2c olur.
Tam bir çember yayının ölçüsü 360°'dir.
O zaman;
2a + 2b + 2c = 360
2.(a + b + c) = 360
a + b + c = 360/2
a + b + c = 180 olur.
Görüldüğü gibi üçgenimizin iç açıları toplamı (a + b + c) 180 derece olarak bulunur.
5. Yol
Bu yöntem göre bir defter veya kağıda çizeceğim üçgenin iç açılarını kesip birleştirmektir.
Yukarıdaki ABC üçgeninde A, B ve C açılarını kesip birleştirelim.
Yukarıdaki şekilde de görüleceği gibi kestiğimiz üç parçayı bir araya getirdiğimizde bir doğru açı oluşmaktadır.
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.