Üslü Sayılar

Üslü Sayı Nedir?

Yukarıdaki matematiksel ifadeye üslü sayı veya üslü ifade denir. İfadedeki a'ya taban, n'e ise üs veya kuvvet denir.

Örneğin; 3², (-5)³, 7⁰, (0,5)¹, (-1)ª ifadeleri birer üslü sayıdır.

Bütün Reel Sayılar Üslü Bir Sayı Şeklinde Yazılabilir

Bütün reel (gerçel) sayılar üslü bir sayı şeklinde ifade edebilir. Bunun için gerekli olan şey bir taban belirlemektir.

Örneğin, 20 sayısını 3 tabanına göre üslü sayı şeklinde yazalım.

Üssün değerini bilmediğimiz için x olarak ifade edelim.

3ˣ = 20

log3ˣ = log20

xlog3 = log20

x = log20/log3

x = 1.30102999566/0.47712125472

x = 2.72683302785 ≈ 2.73 olur.

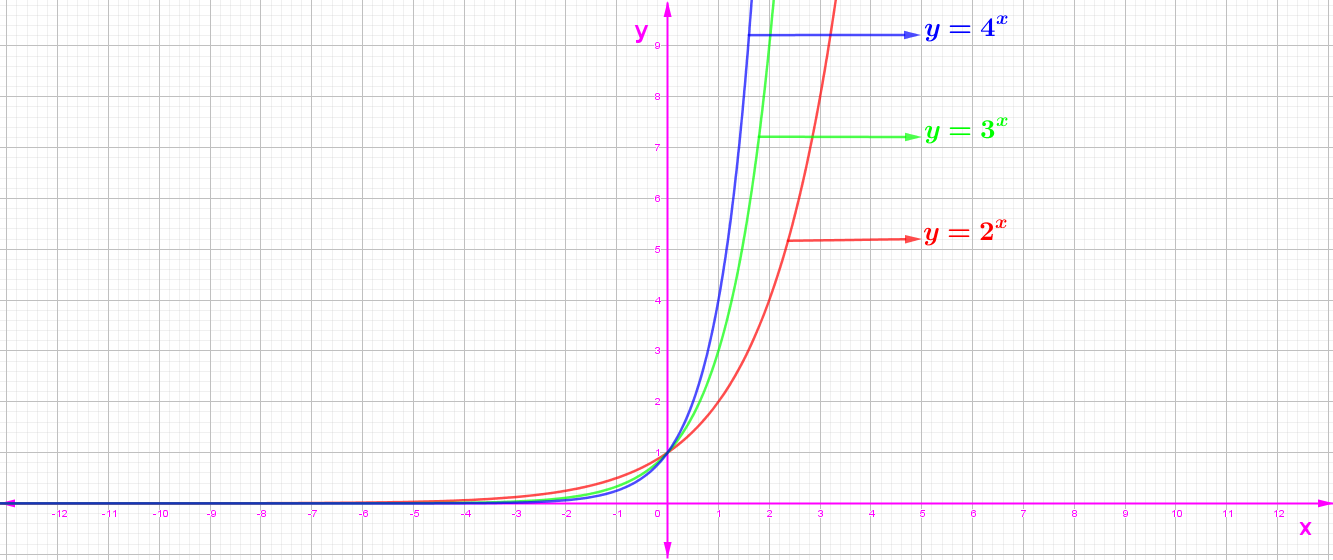
Üslü Sayıların Grafikleri

Yukarıdaki ifade de eğer n pozitif bir tam sayı ise bu a'nın yan yana n kere çarpılacağı anlamına gelir.

2⁵ = 2 . 2 . 2 . 2 . 2 = 32

(-5)³ = (-5) . (-5) . (-5) = -125

(1/2)⁴ = 1/2 . 1/2 . 1/2 . 1/2 = 1/16

Üslü Sayılarda Toplama İşlemi

Ortak üslü ifadelerin önündeki katsayılar toplanır ve ortak üslü ifadelerden biri ile çarpılır.

Örnek

5.7³ + 2.7³ + 4.7³ = (5 + 2 + 4).7³ = 11.7³

Üslü Sayılarda Çıkarma İşlemi

Ortak üslü ifadelerin önündeki katsayılar birbirlerinden çıkarılır ve ortak üslü ifadelerden biri ile çarpılır.

Örnek

9.4² - 6.4² = (9 - 6).4² = 3.4²

Üslü Sayılarda Çarpma İşlemi

Tabanları aynı olan üslü ifadeler çarpılırken üsler toplanır ve ortak tabana üs olarak yazılır.

Örnek

Üsleri aynı olan üslü ifadeler çarpılırken tabanlar çarpılır ve ortak üs aynen yazılır.

Örnek

Üslü Sayılarda Bölme İşlemi

Tabanları aynı olan üslü ifadelerde bölme işlemi yapılırken payın üssünden paydanın üssü çıkarılır ve ortak tabana üs olarak yazılır.

Örnek

Üsleri aynı olan üslü ifadelerde bölme işlemi yapılırken tabanlar bölünür ve ortak üs aynen yazılır.

Örnek

Üslü İfadelerle İlgili Önemli Özellikler

1. Bir sayının sıfırıncı kuvveti 1'e eşittir.

2. Bir sayının birinci kuvveti kendisine eşittir.

3. Sıfırın sıfırıncı kuvveti belirsizdir.

4. Bir sayının 1/n. kuvveti o sayının n. dereceden köküne eşittir.

5. Bir sayının negatif kuvvetinin değeri, 1'in bu sayının pozitif kuvvetine bölümüne eşittir.

6. Negatif üslü bir kesirli ifade ters çevrildiğinde üssü pozitif hale gelir.

7. Üslü bir ifadenin kuvveti alınırken üsler çarpılır.

8. Negatif sayıların tek kuvvetleri negatif olurken çift kuvvetleri ise pozitif olur.