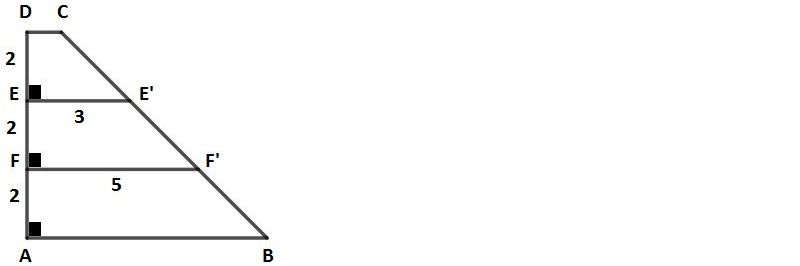yamuğun alanı

Pow
yamuk alan (yamuk alanı) En az iki kenarı birbirine paralel olan dörtgenlere (dört kenarlılar) yamuk denir. Buna tanıma göre; kare, dikdörtgen ve paralelkenar
yamuk alan (yamuk alanı)
En az iki kenarı birbirine paralel olan dörtgenlere (dört kenarlılar) yamuk denir. Buna tanıma göre; kare, dikdörtgen ve paralelkenar birer yamuktur.
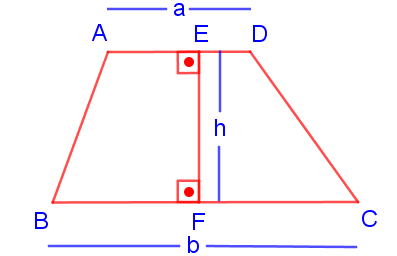
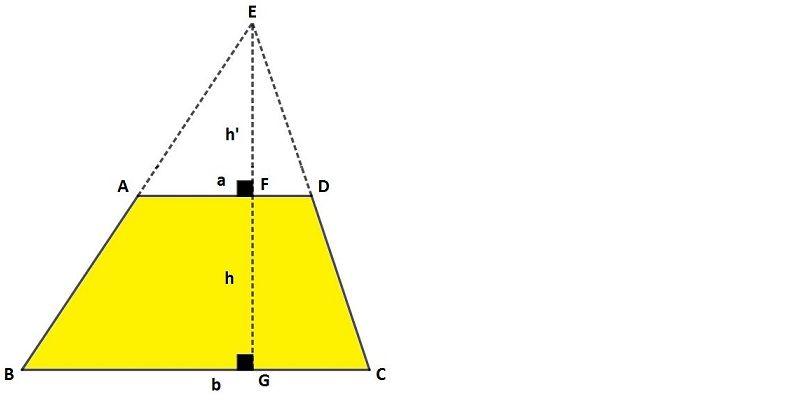
Bir yamukta birbirine paralel olan kenarlara "taban kenar", paralel olmayan kenarlara ise "yanal kenar" denir. Yukarıdaki ABCD yamuğunda [AD] // [BC] olup;
[AD]: üst taban
[BC]: alt taban
[AB]: yanal kenar
[DC]: yanal kenar
[EF]: yükseklik'dir.
yamuğun alanı formülü (yamuğun alan formülü)
Yukarıda şekilde üst taban uzunluğu a, alt taban uzunluğu b ve yüksekliği h olan ABCD yamuğunun alanı;
Alan (ABCD) = (a + b) . h / 2
yamukta orta taban
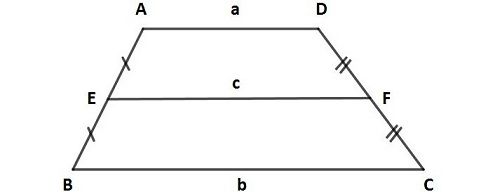
Yukarıdaki ABCD yamuğunda [AB] ve [DC] yanal kenarlarının orta noktalarını birleştiren, [AD] ve [BC] kenarlarına paralel olan [EF] doğru parçasına ABCD yamuğunun "orta tabanı" denir. Orta tabanın uzunluğu alt ve üst taban uzunluklarının toplamının yarısına (ortalamasına) eşittir.
EF = (AD + BC) / 2
Bir yamukta orta taban uzunluğu ile yüksekliğin değeri biliniyor ise bu yamuğun alan orta taban uzunluğu ile yüksekliğin çarpımına eşittir. Yukarıdaki ABCD yamuğu için;
Alan (ABCD) = c . h olur.
yamuk alan formülü (yamuğun alanı nasıl bulunur)
Bir yamuğun alan formülü olan (a + b) . h / 2'nin nereden geldiğini bir çok yoldan ispatlayabiliriz. Aşağı da bu yollardan üç tanesini gösterdik.
1. Yol
Yamuğumuzu alan formülünü bildiğimiz ve alanını kolayca hesaplayabileceğimiz kare, dikdörtgen, paralel kenar ve üçgen gibi geometrik şekillere böleriz.
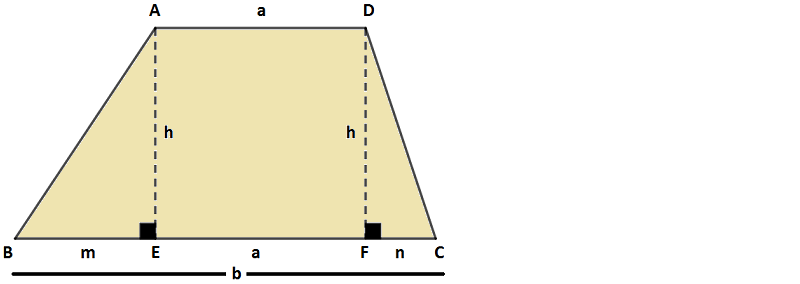
Aşağıdaki şekildeki ABCD yamuğunu alan formülünü bildiğimiz ve alanını kolayca hesaplayabileceğimiz iki tane dik üçgene (ABE ve DFC) ve bir tane dikdörtgene (AEFD) böldük.
Yukarıdaki Şekilde de görüleceği üzere ABCD yamuğunun alanı ABE ve DFC dik üçgeni ile AEFD dikdörtgeninin alanları toplamına eşittir.
A (ABCD) = A (ABE) + A (AEFD) + A (DFC)
İspat
2. Yol
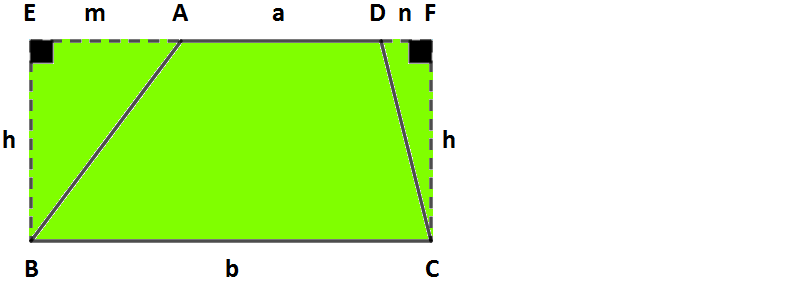
Yamuğumuzu hayali çizgiler yardımı ile bir dikdörtgene dönüştürürüz. Daha sonra dikdörtgenin alanından oluşturduğumuz hayali üçgenlerin alanlarını çıkararak yamuğumuzun gerçek alanını buluruz.
Yukarıdaki şekilde EBCF dikdörtgeninin alanı AEB ve DFC üçgenin alanı ile ABCD yamuğunun alanlarının toplamına eşittir. Buna göre;
A (AEB) + A (ABCD) + A (DFC) = A (EBCF)
A (ABCD) = A (EBCF) - A (AEB) - A (DFC)
İspat
3. Yol
Aşağıdaki şekilde büyük üçgenin (EBC) alanından küçük üçgenin (EAD) alanını çıkarırsak ABCD yamuğunun alanını bulmuş oluruz.
A (EAD) + A (ABCD) = A (EBC)
A (ABCD) = A (EBC) - A (EAD)
Yukarıdaki şekilde ABCD bir yamuk olduğu için [AD] // [BC]'dir ve EBC ile EAD üçgenleri de Açı - Açı - Açı bakımından benzer üçgenlerdir.
EBC ∼ EAD (A . A . A .)
İspat
Yamuğun Alanı ile İlgili Çözümlü Sorular
Örnek 1
|DE| = |EF| = |FA| = 2 cm
|EE'| = 3 cm
|FF'| = 5 cm
|DC| // |EE'| // |FF'|
Şekilde ABCD bir dik yamuk olduğuna göre, alanı kaç cm²'dir.
Çözüm
Yukarıdaki şekilde en küçüğünden büyüğüne DEE'C, DFF'C ve DABC olmak üzere üç tane dik yamuk vardır.
DFF'C Dik yamuğunda [EE'] orta tabandır. Buna göre;
(|DC| + |FF'|) / 2 = |EE'|
(|DC| + 5) / 2 = 3
|DC| + 5 = 3.2
|DC| + 5 = 6
|DC| = 1
EABE' Dik yamuğunda [FF'] orta tabandır. Buna göre;
(|EE'| + |AB|) / 2 = |FF'|
(3 + |AB|) / 2 = 5
3 + |AB| = 5.2
3 + |AB| = 10
|AB| = 7
A (DABC) = (|DC| + |AB|) . |DA| / 2
A (DABC) = (1 + 7) . 6 / 2
A (DABC) = 8 . 6 / 2 = 48 / 2 = 24 cm²
Örnek 2
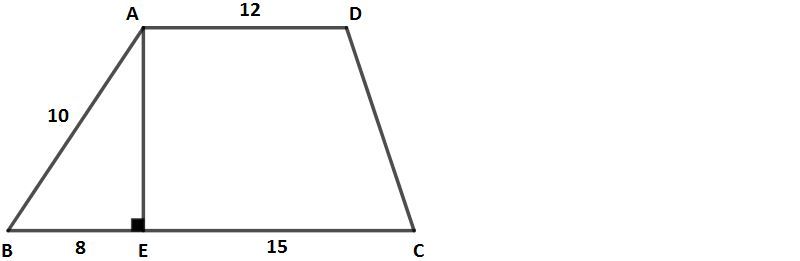
|AD| = 12 cm
|AB| = 10 cm
|BE| = 8 cm
|EC| = 15 cm olmak üzere yukarıdaki şekildeki ABCD yamuğunun alanı kaç cm²'dir.
Çözüm
İlk önce ABE dik üçgenine Pisagor teoremini uygulayarak yamuğun yüksekliğini buluruz.
|AE| = h olsun
|AE|² + |BE|² = |AB|²
h² + 8² = 10²
h² + 64 = 100
h² = 100 - 64
h² = 36
h = 6 olur.
A (ABCD) = (|AD| + |BC|) . h / 2
A (ABCD) = (12 + 23) . 6 / 2
A (ABCD) = 35 . 6 / 2
A (ABCD) = 210 / 2 = 105 cm²
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.