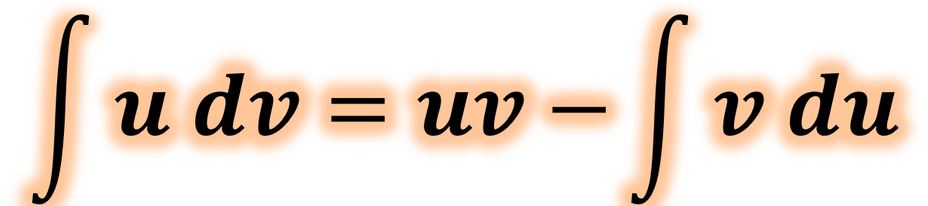kısmi integral yöntemi

kısmi integral yöntemi nedir ?

Kısmi İntegral Yöntemi, integral alma yöntemlerinden biri olup; genellikle polinom şeklindeki bir fonksiyon ile üstel veya trigonometrik bir fonksiyonun çarpımının integralini almak için kullanılır.

Tek parça halindeki bazı fonksiyonların integralini almak oldukça zor ve zaman alıcı bir iş olduğundan parçalı integral yöntemi ile bu durumdaki fonksiyonlar, parçalarından birisinin kolayca integralinin alınabileceği iki parçaya ayrılır. $x^2.sinx$, $3x.lnx$, $x^3.e^x$ bu türden fonksiyonlara örnek olarak verilebilir.

türev ve diferansiyel ilişkisi

$y=f(x)$

$dy=df(x)$ (eşitliğin her iki tarafının da diferansiyelini alırız)

$dy=f^{\prime }(x)dx$

$\frac{dy}{dx}=\frac{f^{\prime }(x).\cancel{dx}}{\cancel{dx}}$

$\frac{dy}{dx}=f^{\prime }(x)$ olur.

Yukarıdaki eşitlikteki "dx" ve "dy" ifadeleri sonsuz küçüklükteki (sıfıra çok yakın) değişiklikleri ifade etmektedir.

kısmi integral formülü

u ve v türevlenebilir (türevi alınabilir) iki fonksiyon olsun.

$\int u.dv=u.v-\int v.du$ olur.

kısmi integral formülünün ispatı

$(u.v{)}^{\prime }=u^{\prime }.v+v^{\prime }.u\Rightarrow d(u.v)=du.v+dv.u$ olur. (bakınız çarpımın türevi)

$d(u.v)=du.v+dv.u$

$d(u.v)=v.du+u.dv$

$v.du+u.dv=d(u.v)$

$\int (v.du+u.dv)=\int d(u.v)$ (eşitliğin her iki tarafının da integralini alırız)

$\boxed{\int df(x)=\int f^{\prime }(x)dx=f(x)+c}$

$\int (v.du+u.dv)=u.v$

$\int v.du+\int u.dv=u.v$

$\int u.dv=u.v-\int v.du$

Örnek 1

$\int x.sinxdx$ integralinin sonucu neye eşittir ?

$x=u$ ve $sinxdx=dv$ olsun.

$x=u$

$dx=du$

$sinxdx=dv$

$\int sinxdx=\int dv$

$-cosx=v$

$\int u.dv=u.v-\int v.du$

$\int x.sinxdx=x.-cosx-\int -cosxdx$

$\int x.sinxdx=-x.cosx+\int cosxdx$

$\int x.sinxdx=-x.cosx+sinx+c$

Örnek 2

$\int 3x^2.lnxdx$ integralinin sonucu neye eşittir ?

$lnx=u$ ve $3x^2=dv$ olsun.

$lnx=u$

$d(lnx)=du$

$(lnx{)}^{\prime }dx=du$

$\frac{(x{)}^{\prime }}{x}.dx=du$

$\frac{1}{x}.dx=du$

$\frac{1.dx}{x}=du$

$\frac{dx}{x}=du$

$3x^2=dv$

$\int 3x^{2}dx=\int dv$

$x^3=v$

$\int u.dv=u.v-\int v.du$

$\int lnx.3x^{2}dx=lnx.x^3-\int x^3.\frac{dx}{x}$

$\int lnx.3x^{2}dx=lnx.x^3-\int \frac{x^3.dx}{x}$

$\int lnx.3x^{2}dx=lnx.x^3-\int x^{3-1}.dx$

$\int lnx.3x^{2}dx=lnx.x^3-\int x^{2}dx$

$\int lnx.3x^{2}dx=lnx.x^3-\frac{x^3}{3}+c$

Örnek 3

$\int 2x.e^{x}dx$ integralinin sonucu neye eşittir ?

$2x=u$ ve $e^{x}dx=dv$ olsun.

$d(2x)=du$

$(2x{)}^{\prime }dx=du$

$2dx=du$

$e^{x}dx=dv$

$\int e^{x}dx=\int dv$

$e^x=v$

$\int u.dv=u.v-\int v.du$

$\int 2x.e^{x}dx=2x.e^x-\int e^x.2dx$

$\int 2x.e^{x}dx=2x.e^x-2.\int e^{x}dx$

$\int 2x.e^{x}dx=2x.e^x-2.e^x+c$

$\int 2x.e^{x}dx=2e^x.(x-1)+c$