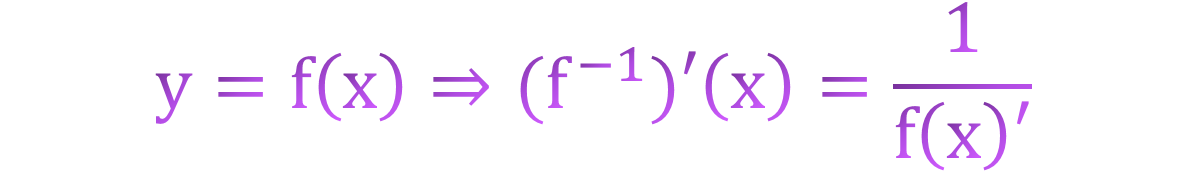f: A → B'ye tanımlı bire bir ve örten bir fonksiyon olmak üzere; f⁻¹: B → A'ya tanımlı fonksiyonuna f fonksiyonun ters fonksiyonu denir.
y = f(x) ⇒ x = f⁻¹(y) olur. Eşitlikteki f⁻¹(y)'ye f(x) fonksiyonun ters fonksiyonu denir ve f⁻¹(x) şeklinde de gösterilebilir.
Ters Fonksiyon Türevi Formülü
(f⁻¹)'(y) = (f⁻¹)'(f(x)) = 1/f(x)' (f(x)' ≠ 0)
Ters Fonksiyon Türevi İspatı
f(x) = y
f⁻¹(y) = x
y = f(u) ⇒ y' = u'.f(u)'
f⁻¹(y)' = x' (eşitliğin her iki tarafının da türevini alırız)
y'.f⁻¹(y)' = 1
f⁻¹(y)' = 1/y'
f⁻¹(y)' = 1/f(x)' olur.
Örnek 1
y = f(x) = 2x + 3 ise (f⁻¹)'(x) = ?
1. Yol
y = f(x) = 2x + 3 fonksiyonunun tersini bulabilmek için x yerine y ve y yerine de x koyar ve y'yi yalnız bırakırız. (bakınız ters fonksiyon)
2x + 3 = y
2y + 3 = x
2y = x - 3
y = (x - 3)/2
f⁻¹(x) = (x - 3)/2 = 1/2.(x - 3)
(f⁻¹)'(x) = 1/2.(x - 3)'
(f⁻¹)'(x) = 1/2.1
(f⁻¹)'(x) = 1/2 olur.
2. Yol
(f⁻¹)'(y) = 1/f(x)'
f(x) = 2x + 3
f(x)' = (2x + 3)'
f(x)' = 2
(f⁻¹)'(y) = 1/2
(f⁻¹)'(x) = 1/2 olur.
Örnek 2
y = f(x) = x² ise (f⁻¹)'(x) = ?
1. Yol
x² = y
y² = x
√y² = √x
y = √x
f⁻¹(x) = √x
(f⁻¹)'(x) = (√x)'
(f⁻¹)'(x) = 1/2√x olur. (bakınız karekök türevi)
2. Yol
(f⁻¹)'(y) = 1/f(x)'
f(x) = x²
f(x)' = (x²)'
f(x)' = 2x
(f⁻¹)'(y) = 1/2x
x² = y
√x² = √y
x = √y
(f⁻¹)'(y) = 1/2√y
(f⁻¹)'(x) = 1/2√x olur.
